Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Verschieben von Funktionsgraphen: Unterschied zwischen den Versionen
K |
|||
| (25 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | + | <div style="padding:1px;background:#1C86EE;border:0px groove;"> | |
| − | + | ||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | {| | ||
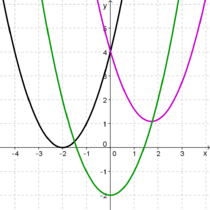
| + | | valign="top"|In der 9. Klasse lernst du, welchen Einfluss die Parameter '''<span style="color: #FF7F00 ">a</span>''', '''<span style="color:#FF7F00 ">b</span>''' oder '''<span style="color:#FF7F00 ">c</span>''' auf eine Parabel, also auf den Graphen einer quadratischen Funktion mit dem Funktionsterm<br /> | ||
| + | f (x) = '''<span style="color:#FF7F00 ">a</span>'''x<sup>2</sup> + '''<span style="color: #FF7F00 ">b</span>'''x + '''<span style="color: #FF7F00 ">c</span>''',<br /> | ||
| + | haben.<br /> | ||
<br /> | <br /> | ||
| + | Oft wird auch die Scheitelform einer quadratischen Funktion<br /> | ||
| + | f (x) = (x - '''<span style="color:#FF7F00 ">d</span>''')<sup>2</sup> + '''<span style="color: #FF7F00 ">e</span>'''<br /> | ||
| + | betrachtet.<br /> | ||
| + | In diesem Fall sind die Parameter '''<span style="color: #FF7F00 ">d</span>''' und '''<span style="color:#FF7F00 ">e</span>''' ausschlaggebend für die Lage der zugehörigen Parabel. <br /> | ||
<br /> | <br /> | ||
| − | + | Dieses Wissen kannst du [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Wiederholung: Verschiebung von Parabeln| hier]] noch einmal auffrischen. | |
| − | + | ||
| − | + | ||
| − | + | |width="3%"| | |
| − | + | | [[Datei:Verschiebungen von Parabeln.png|210px|verweis=Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Wiederholung:_Verschiebung_von_Parabeln]] | |
| − | + | ||
| − | + | |} | |
| − | # | + | </td></tr></table></center> |
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background:#1C86EE;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | <big>Aber auch andere Funktionsgraphen lassen sich derartig verschieben.<br> | ||
<br /> | <br /> | ||
| − | + | Im Folgenden wollen wir '''allgemein''' untersuchen, welchen Einfluss Parameter in einer Funktionsgleichung auf den Verlauf des Graphens der Funktion haben.<br> | |
| + | <br /> | ||
| + | Arbeite dich entlang des [http://wikis.zum.de/projektwiki/Datei:AB_Verschieben.pdf Arbeitsblattes] zum Thema "Verschieben von Funktionsgraphen" durch die drei Unterkapitel!</big> | ||
| + | |||
{| | {| | ||
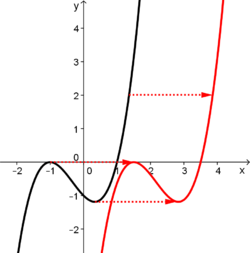
| − | | [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- Richtung|Verschiebung in x- Richtung]] | + | |valign="top"| [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- Richtung|<big><center>Verschiebung in x- Richtung</center>]] |
| − | [[Datei:Verschiebung | + | [[Datei:Verschiebung in x- Richtung.png|250px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Verschiebung_in_x-_Richtung]] |
|width="3%"| | |width="3%"| | ||
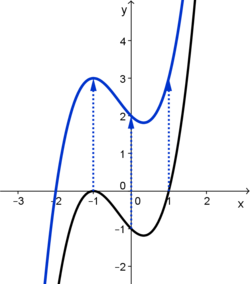
| − | | [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in y- Richtung|Verschiebung in y- Richtung]] | + | |valign="top"| [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in y- Richtung|<big><center>Verschiebung in y- Richtung</center>]] |
| − | [[Datei:Verschiebung | + | [[Datei:Verschiebung in y- Richtung.png|250px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Verschiebung_in_y-_Richtung]] |
|width="3%"| | |width="3%"| | ||
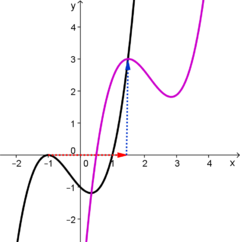
| − | | [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- und y- Richtung|Verschiebung in x- und y- Richtung]] | + | |valign="top"| [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- und y- Richtung|<big><center>Verschiebung in x- und y- Richtung</center>]] |
| − | [[Datei:Verschiebung | + | [[Datei:Verschiebung in x- und y- Richtung.png|240px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Verschiebung_in_x-_und_y-_Richtung]] |
| + | |} | ||
| + | |||
| + | {| | ||
| + | {{Vorlage:Lesepfad Ende | ||
| + | |Link zurück=[[Manipulationen an Funktionen|Zurück zur Übersicht]] | ||
| + | |Link vor=[[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- Richtung|Los geht´s mit der Verschiebung in x- Richtung]] | ||
| + | |Text Copyright=<colorize>Manipulationen an Funktionen</colorize> | ||
| + | }} | ||
|} | |} | ||
Aktuelle Version vom 15. August 2013, 15:43 Uhr
|
|
Aber auch andere Funktionsgraphen lassen sich derartig verschieben.
Manipulationen an Funktionen
|