|
|
| (10 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| − | Bei ganzrationalen Funktionen ist der '''Grad der Funktion''', sowie das '''Vorzeichen des Leitkoeffizienten''' ausschlaggebend, zu welchem der vier charakteristischen Verläufe die Funktion gehört:<br /> | + | __NOTOC__ |
| | + | <div style="padding:1px;background:#66CD00;border:0px groove;"> |
| | + | |
| | + | |
| | + | <center><table border="0" width="850px" cellpadding=5 cellspacing=15> |
| | + | <tr><td width="800px" valign="top"> |
| | + | <big>Der charakteristische Verlauf von ganzrationalen Funktionen ist von zwei Faktoren abhängig. Worauf es genau ankommt, kannst du im folgenden Applet mit den Schiebereglern untersuchen.<br /> |
| | + | Welche '''vier Fälle''' unterscheidet man?</big> |
| | + | <br /> |
| | + | <center> |
| | + | <ggb_applet width="585" height="489" version="4.2" ggbBase64="UEsDBBQACAAIAPmLEEMAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAD5ixBDAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbM1Y62/bNhD/nP4VB30Y2i2xRVEvd3aLrkCxAklXLFnRbdgAWqJtNrKkiZQfRf/4HR+yZSfN1mQolsTmQ8e7+92Lp4yfb5YFrHgjRVVOPDLwPeBlVuWinE+8Vs3OUu/5s0fjOa/mfNowmFXNkqmJFw4Cb38OVwMa68Min3jJNPTzjORnAefsLAxJdjYKkuCMxFkcBCQM83TmAWykeFpWb9iSy5pl/DJb8CU7rzKmDM+FUvXT4XC9Xg866YOqmQ/n8+lgI3MPUPNSTjw3eYrsDg6tqSEPfJ8M31+cW/ZnopSKlRn3QKNqxbNHJ+O1KPNqDWuRq8XEiwkiW3AxXyDM2EdMQ01UI9aaZ0qsuMSjvaXBrJa1Z8hYqZ+f2BkUOzge5GIlct5MPH9AgzgZJTSN4sAfkcgPPagawUvliIkTOuzYjVeCry1fPTMiQ3+UoA+EFNOCT7wZKyTCEuWsQZOiRk2LS6m2BZ+yplvvFSKn+IsE4iPXvBCntcPEo5SepqPTxPdPo8jh78v1QFVVYZj6EI3g0ycI/MCHUz0QOwQ4xLF95Ns9n9ohsENoh8jShPZ4aElDSxNampDeAdOt9zjdxgHQDibtwySIT3/Qx6ehfxNn2sNJNIhPQLT2ZqCg9SZGfz2EbhnbZWIG4tuBuIep/jL2ih+IiN4LEelJteHweaE3wqWTGKXRv5cYPAjnDmVwG8og+gzKBxq3E0qinlCUZf7M54ZI+kU4P2vaL5AYhw9J/XsITPyDtO9y3o7EjXeZ4T9TajzsiuHYKQRyoWldSCu+lFpFOjLFCQhEmLxxgrUkAjLCIdFJHACJIIxwSVKI9ZgA1XkbAoUUNB2hYEpQlOJXaHI6hgh56c3EJjfQECIKxBSuENAKYIof2iSgSBFFEOEhLZ1osTSGMMYFTSFEBXXZS3RpoXgO1yg8AEqA6rMkgSCGOIBEl04S6ooap1p3ZBpA7EOsj2LtxLppayaeSIFqNJgFdSXFzrgLXtQ7rxg7irJulbOd28+WeWdHVR2R51V2/cORsTmTqpsjEV5Y+3vRXmAH1+bJuGBTXmBzcanjAGDFCp3mhv+sKhV0MRDbvXnD6oXI5CVXCk9J+MBW7JwpvnmF1LJT0Ig2t/mYt1khcsHKdxgkmoVmCN3lbopXd7mHMbFSsqpq8sutxMiBzW+8qbDiBMFg1P9BC27dIxoM/P4PWlpmTMd8ODo8hPfz1j2K/MNDTjRf7aCxDZedLeeNyPvz1/KHqsh3/qgrUaqXrFZtYxo1LJSNxvSinBfcmNaUXmx5sutptbm0NqWW19W2xpVv5U/nL6uiagATMojQNnM3Tu1oaLRiOyrf0PiGwu+cJPLdczIKDIUZp3Y0VOh1q5oDSjqUxO/ECGlKDTLvx5gJmYm38aAthTq3K4xPkV07qMQeeNMupxhu7twhT3Irz+19eGqtsZmT6r1rmPX81978asEV021eFNBolCZJhN/BKE1tnB5F6PiaNyUvbByWGApt1UqbGLvgPhm3kr9lavGizH/mc0zpt0xXVYWqWdK9ejnPxBIP2n1nfKYD4xeEandzPm94Z6LC9NbWNeap38+KG9uG1aumWr4uV1cYdUeqjocdnrHMGlHr2IYplvlrvo9ftBLDSyLvn0PwElFkumChI5R2wssFwrxGlGhVITGcG3jHm4K1+P7AWrWoMOAuto1gSzhHvZAxlgZdPeBFO2+lwmqMUa+rQsGX2F6DMrFftktkme3CgJnWHXG0Dqp2pQGrQwCq6QesYEehszc4Pv5MdgAr6oWJBJftBdsihL41DbeLKu8EO7GFflOApcDSfYbZuGQbrCDIbyqrolX4roTuK/fvSlYzV+OwN9KRiCdoQvVsi71soCczseG7soLGEx8x4A6jZ5+lCuvuNb59SFNKlCsaZvKjyHNe7rRlJQaccRtW0NqQY83nNut2B2sEb4pVL1ScW/7RQdNjB8X/IwcR5x/iP8BBhH5ND5H7eGhTNyhLM3EWxiTETRwfb57ABBh8C5s/H0+fwHdmhDMgT2xbcOjdWVuaLPf2jO52Za8O9n3ZXVg3venf6c2fZjPJlbZ/lBrjdxfd7b6+1eDRXQa/22xXfKOIM903f7WV+t4Z0C7Qeo/P2RV///vsD21Ku2u/b7Mm9kLKO+T9Va25t5fbNTF8fCsJaTAdb5ueT2Kuz3YvCNirXLjL1PaCvntr2CefYo16q1sg0E7ERs26kQyi8KDHwvbr466Y950y7F82pnd0/2F69jdQSwcI6qlu55oGAAAREwAAUEsBAhQAFAAIAAgA+YsQQ0XM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAD5ixBD6qlu55oGAAAREwAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAADIHAAAAAA==" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" useLocalJar="true" /> |
| | + | </center> |
| | + | <br /> |
| | + | <popup name="Lösung"> |
| | + | Bei ganzrationalen Funktionen ist der '''Grad der Funktion''', sowie das '''Vorzeichen des Leitkoeffizienten''' dafür ausschlaggebend, zu welchem der vier charakteristischen Verläufe die Funktion gehört:<br /> |
| | + | <br /> |
| | | | |
| | {| | | {| |
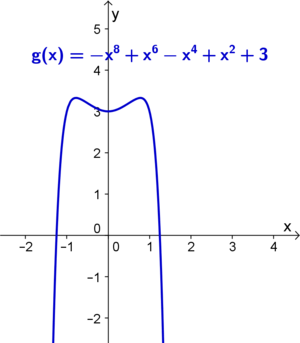
| − | | valign="top"|<big><center>'''<span style="color: #00BFFF ">"von links oben nach rechts oben"</span>'''</center><br /> | + | | valign="top"|<big><center>'''<span style="color:#00BFFF">"von links oben nach rechts oben"</span>'''</center></big><br /> |
| − | <ggb_applet width="360" height="442" version="4.2" ggbBase64="UEsDBBQACAAIAIJtvUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAIJtvUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVfhbts2EP7dPsVBP4Z2i21SpCi5s1u0BYoVSLpiyYZiPwZQEm2zkSVPom256J8904A9wB5lT7IjKdmO0xZIAxSJRZE83t13vPtITZ61ywI2qm50VU4DOiQBqDKrcl3Op8HazAZJ8Ozpw8lcVXOV1hJmVb2UZhrwYRgc1mFvyGO7WOfTQKRxlKaMDlIu+YCTsRjInGSDOIy4jBTLRCgDgLbRT8rqjVyqZiUzdZkt1FKeV5k0TufCmNWT0Wi73Q5768Oqno/m83TYNnkA6HnZTIPu5Qmqu7Foy5x4SAgdvbs49+oHumyMLDMVgEW11k8fPphsdZlXW9jq3CymAUvGASyUni8QZiRoACMrtEKsK5UZvVENLj3qOsxmuQqcmCzt/AP/BsUeTgC53uhc1dOADEUYUhKPxZhGVMRooqq1Kk0n2psc9comG622Xqt9cwYxrDHugG50WqhpMJNFg6B0OasxoOhPvcZuY3aFSmXd9w/u0DP8QwH9QVlduHM+Cog/Jmc0is9iQs6iiHhfjg0HYKqqcFoJRGP4+BFCEhI4sw31TYiNEH6K+DHCfBP6hvsm8jLcL+delHsZ7mU4+wLOrn8A2g3cQNrjZMc4KeKzP4E/F4ATnMkRTmpBfARqvXcNA+s3df7bhndd4buxayjxDe0mE/tw8RL3RMS+ChE9surz4fNGb+XL3qK4g8XwXjj3KEMe3rYZRp9Bec/g9kZpdAQUbbl/97tlkt0J52dDeweLgt+n9r/CYEy+hcHJqGe6SVd70CysbJeuRi0byzps7IgHKERYmCJGnoiAjrGJbYGGQCPgEXZpAsK2MTBbkxwYJGDlKANHL1GCD+7qVUCEuuxg7AsXGIeIAXWkxAGpCByxIcmFDCWiCCJcZK1Ta5YJ4AI7LAGODlpKiy1tMFyHfTQeAqPA7FoaQyhAhBBbWqTcsqVIrO+oNARBQNilyIvIiZ4PcUUCzKLBDF9Vjd4Hd6GK1X5XXBx1uVqbLnbdeLbM+zia6kQ8r7LrFyfBVrIx/TsK4Wl0OPL86XTjRHwwKWSqCrw3XNo8ANjIwpaw0z+rSgN9DiR+bF7L1UJnzaUyBlc18F5u5Lk0qn2F0k3voDPtDuqJWmeFzrUsf8MksSqsQtif25aY+nObU+6tZFVV55e7BjMH2t9VXaEDjA8F5xQPUM7xhIujAHZ+KkzYkEfjUAgREYZCmLiZtCkf0SFjHK8DCRkncRjjHWF3cyqhguK5SXiHT232yGSrmj6U89qWUxd823ndvKiKw9Cq0qV5KVdmXbs7GJJgbTE9L+eFcqF1tIq3mew6rdpLH1PmdV3tVtgj3oF0/rIqqhqwIMMIMc67NvWtk7Ge7aWIkyFOgvSbpPP9PB2HTsK1qW+dFO66d61DSnuYlPRmdONoBJUf55hLmWnQBrAutTn3PcxPnV13UKlf8Ga9TDHdunU3ddJP6tzdXedkdJJhk2tVl6rweVTiXq6rdeMTe5+cDybrRr2VZvG8zH9RcyzJt9KyokHVXvTgcq4yvcSFfrwLnrQb+yu66kdzNa9VD7Fw114fWjdLjrP61rBT9aqulq/LzRVmzYmrk1GPZ9JktV7Z5IQUafpaHfIv141Eks+P1yH4BlFklnAwkMYGsUpVObCPAOTaLCrMj4tdreUSztEN1IOVjBjHcCE1MidmqK3gdlWrxn4z+G0CtIJM01o6etQ+hiny8/fQ/vFIPIYBsrV7Z4/hB2ixT50zqlBLvCuDcbk+W5fOrf2+z9w13O4vVOl7pKeTvDjaOJw/yX0asX19gCxWC2lv6110C7lT9Y14O5U/z2aNMtBOg4HAO+MOyYcdTV9UebdJtONC3ar8NDMOFWSQE6/x2o95iT6YrqDdy086z1XZKcJk9YH4RFinwZVqDe0i+92f68r82Me3/e+vf2xs23//7sPqBT4RXORiE9xU+Y2De4ge+UL0dHMur9S702F36jSq1rP9FQXZ8qL7zPWnEenuLfvtwc/D2ry1JAxuT8lwjN+tSPwsiUXMQ0u1do+HYiyiMYuikCScczwPPnjFJ3szOi4ed5Z1H7NP/wdQSwcI/tdYIQ4GAAB8DwAAUEsBAhQAFAAIAAgAgm29QtY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACACCbb1C/tdYIQ4GAAB8DwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAKUGAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
| + | [[Datei:Oben-oben.png|300px]] |
| | |width="1%"| | | |width="1%"| |
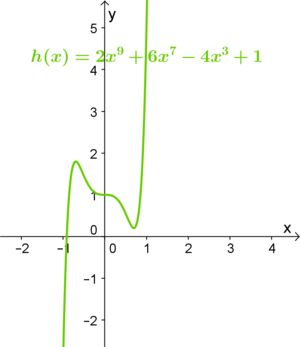
| − | | valign="top"|<big><center>'''<span style="color: #9ACD32 ">"von links unten nach rechts oben"</span>'''</center><br /> | + | | valign="top"|<big><center>'''<span style="color:#9ACD32">"von links unten nach rechts oben"</span>'''</center></big><br /> |
| − | <ggb_applet width="360" height="444" version="4.2" ggbBase64="UEsDBBQACAAIAJNtvUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAJNtvUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVfdbts2FL5un+JAF0O7xTapf3V2i65AsQJJUSzZUOxiAC3RNhtZ1ETKlove7Jl2Mex2j7In2SEp2Y6bDEgDbHHsI1Lnn+d8JKcvunUJG94oIauZR8fEA17lshDVcua1ejFKvRfPH0+XXC75vGGwkM2a6ZkXjn3vIIejcZgYYVHgKM1omJBkxJGOwriIRimfpyNCFjSJyIL4EfMAOiWeVfItW3NVs5xf5iu+ZucyZ9rqXGldP5tMttvteLA+ls1yslzOx50qPEDPKzXz+odnqO6G0Daw7D4hdPL+4typH4lKaVbl3AMTVSueP3403YqqkFvYikKvZl6QZh6suFiuMMwoDjyYGKYaY615rsWGKxQ9GtqY9br2LBurzPtH7gnKfTgeFGIjCt7MPDKOaEiDNKVJmJKEZqkHshG80j0v7W1OBm3TjeBbp9Y8uSyTLMElEErMSz7zFqxUGJWoFg1mFB1qWhwqvSv5nDXD+OAPPcMPMoiP3OjCpXNpmHlJGJ75UXyWEHIWRcT5cmzYAy1labUSiDL49Al84hM4M4Q64iOJY/eKuDkSOOI7EjoSOZ7QiYeONXQ8oeMJg3+Jsx8fAu0nbkQ6xBkcx0kxPvON8WsTcBJnehQnNUF8Amq8tyQA4ze1/hsS9sPYDRNLKHGE9i9T82PzFT8wouCLIqJHVl093G30s3rZW4zvYdF/UJz7KP3bovSjO6J8YHIHozQ6Moq27L/9fmYyuFecd6b2Hhbj8CG9/wUGE/JfGJxOBqSb9r0HamV4+3LVfK0M6gSZBR6gEGFjxgniRAQ0Q5KYBvWBRhBGOKQpxIYmEJieDCGAFAwfDcDCS5TiT2j7NYYIdZnJxDUuBCFEAVALSiEgFIEFNgQ5P0COKIIIhYx1aswGMYQxDoIUQnTQQFpiYCNAORyjcR8CCoGRpQn4McQ+JAYWaWjQMk6N76jUh5hAbEQRFxETHR6iRAqBiQYrvJZK7JO74mW9XxWbR1HVre5z18/n62LIo5Yn7IXMr787STZnSg/PyIS70WHPc7vTjS3x0bRkc17iweHS1AHAhpWmha3+haw0DDWQurllw+qVyNUl1xqlFHxgG3bONO9eI7caHLSm7U495W1eikKw6icsEqPCKIT9xm2Aadi4Q0QBayWXsikudworB7qfeSPRAT8a4+aWJXFCMj+kBDf8nXvlp8E4yII4TbMoihPftJnKman5MBtnx3+4PezufGVN880+NNZxNeRy2Zh+6rNvBm/Ud7I8TNVSVPoVq3Xb2FMYomBjgnpZLUtuc2txFc8z+fVcdpcuqYHTdbWrcUScA/PlK1nKBrAj/ShChp7OHbU8xrM9F7E8xHKQYZVEsX9PM99yWDp31HLhsjvX+kjpECYlgxmhLI6g8uMiszUz8zoP2kroczfCAhX5dR8qdQJv2/Uc662Xu6mT3qpzd3+d08lJiU2veVPx0hVShWvZyla5yt5X56Npq/g7plcvq+IHvsSefMcMLGpU7VgPLhc8F2sUdPN98phZ2B/RVTdb8GXDhxBLe/B1qbVvyXFZfzZtVb1u5PpNtbnCqjlxdToZ4pmqvBG1KU6YI05f80P9FUIxRPniWA6DVxhFbhAHE6lNEttK82ok57zygLV6JbFALnaNYGs4Rz9QEfYyBpnBBROInViipoe7uuHKXBvcOgEe2hFrOgSk1ZPuKcwQvL+G7pcn2VP4BmL3nDyFEWK3fQ7MPLVe8ZKv8dQM2hb9oq2sf/sCWNkTuVlokPMPCFQnBXK0gvj+UOTEFTkePPtGAFbWK2YO7n2aS7bjzY3EW5UXsuiXgw7Lgattc4b4UxsFpvJqzl3R6r5ZoUaFttePXDq0lEaUvMaLABZqdCRkHr4XRcGr3h5Wr0vILWmeeVe807TP9Fe/tlJ/O+S7+/u3P02ukf5h8tz99btJsWO6JdGI0Nq7qfZ/S3Q/uxAdL06bTahzdsXfn07bvUjxRiz2BxeE0Iv+9uv2KNKfZvYribfGRr8zyIwX15k3ouOU4O4Qxn5KsgwvcrgbmHtwTNOjD17QPjq9J8szOW4ou8H1V9zn/wBQSwcIDSs85Q4GAACSDwAAUEsBAhQAFAAIAAgAk229QtY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACACTbb1CDSs85Q4GAACSDwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAKUGAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
| + | [[Datei:Unten-oben.png|300px]] |
| | |- | | |- |
| | | <br> | | | <br> |
| | |- | | |- |
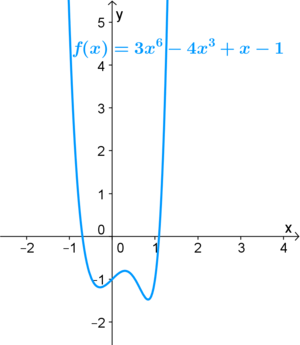
| − | | valign="top"|<big><center>'''<span style="color: #0000CD ">"von links unten nach rechts unten"</span>'''</center><br /> | + | | valign="top"|<big><center>'''<span style="color:#0000CD">"von links unten nach rechts unten"</span>'''</center></big><br /> |
| − | <ggb_applet width="363" height="443" version="4.2" ggbBase64="UEsDBBQACAAIAGFvvUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAGFvvUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVdfj9s2DH++fgrCD0OLXRLJkmW7S1q0A4oVuCuK3W0o9jBAsZVEPcfObDl/ir70Kw3DsOd9lH6SUZKd5NJrsbbAlruEpkSR/FEkJY8fb5cFrFXd6KqcBHRIAlBlVuW6nE+C1swGSfD40b3xXFVzNa0lzKp6Kc0k4MMwOKxDbshju1jnk4CEcShimQ4kIdGAizAbpBEnAzETXCkx41maBADbRj8sqxdyqZqVzNRVtlBLeVFl0jidC2NWD0ejzWYz7K0Pq3o+ms+nw22TB4Cel80k6B4eorpbizbMiYeE0NGrywuvfqDLxsgyUwFYVK1+dO9svNFlXm1go3OzmAQsRWQLpecLhBkJZEZWaIVYVyozeq0aXHrEOsxmuQqcmCzt/Jl/gmIPJ4Bcr3WuaozPMKIkJJwkVLBQRIwGUNValaaTpZ3NUa9tvNZq49XaJ2eRkzTGLdCNnhZqEsxk0SAqXc5qjCg6VLfINmZXqKmse/7gDz3HPxTQb5TVhVvnwzAJYpKe0zg8jwk5jyLifTk2HICpqsJpJRCl8PYthIgHzi2hnoRIhPBTxI8R5knoCfck8jLcL+delHsZ7mU4+wTOjj8A7QZuIe1xsmOcFPHZr8CvC8AJzuQIJ7Ug3gK13jvCwPpNnf+W8I4Vno0docQT2k0m9sfFS3wlIvZFiOiRVZ8PHzf6Qb7sLQr27y2GX4VzjzK8C2UYfQTlVwa3N0qjI6Noy/277wcm2Wfh/GhoP8Oi4F9T+19gMCb/hcHxqO904672oFlY2S5djVo2tuuw1DUeoBBhYYoY+0QENEUS2wINgUbAI2RpAsLSGJitSQ4MErBylIFrL1GCP9zVq4AIddnB2BcuMA4RA+qaEgdsReAaGza5kKFEFEGEi6x1as0yAVwgwxLg6KBtabFtGwzXIY/GQ2AUmF1LYwgFiBBi2xYpt91SJNZ3VBqCICDsUuyL2BN9P8QVCTCLBjN8VTV6H9yFKlb7XXFx1OWqNV3suvFsmfdxNNWJeF5lN09Pgq1kY/pnFMLT6HDm+dPp1pF4Ni7kVBV4cbiyeQCwloUtYad/VpUG+hxI/Ni8lquFzporZQyuauC1XMsLadT2GUo3vYPOtDupx6rNCp1rWf6MSWJVWIWwP7htY+oPbk4jbyWrqjq/2jWYObD9RdUVOsDIMKFhShOWRkwk9nzZ+akw4cM4TOI4YpFIYo6BbjJpUz4iQ+I+nIY4Q1NcczrVfSj3ptV6D01uVdPHcl7beuqib5nnzdOqOAytKl2a7+XKtLW7haF3tQX1pJwXysXW9VW8z2Q302p75YPKvK7r3Qo54h2Yzr+viqoGrMgwilCgo1NPnYz1bC9FnAxxEqTfJZ3v56m9G807OvXUSeG2e9c6pLSHSUlvRjf+chjcSjKXM5NgG0BbanPhOUxQnd10UKlf8KJdTjHfunW3ddI7de4+X+d4dJJi4xtVl6rwiVTiXrZV2/jM3mfn2bht1EtpFk/K/Ec1x5p8KW1bNKjaix5czlWml7jQj3fBk3Zjf0JX/Wiu5rXqIRbu4utD62bJcVp/MOxUPaur5fNyfY1Zc+LqeNTjGTdZrVc2OWGKffpGHfIv143ELp8fr0PwDaLIbMfBQBobxLY0qhy43wBkaxYVZsjlrtZyCRfoCGrCYkaUKVxKjc0Tc9QW8XZVq8a+N/iNgkmAojiK9P72AUxgsP31fvIAvgWk4gEMLOUdH1rqmspYFWqJd2YwLuVnbem822//3N3H7TZDNX2NbeokPY72D+fvLAG8eiKyYrWQ9tLehbiQO1XfCrpTeFnl3VbQruXprcpP9/9QJwZb3w3e7jH7sCJNV7bu4Qed56rsFGFKepx3hG4SXKutoV30vvmtrcx3+xi+f/eXDdn7d3/aCL5/94fl/v7dhs9L3hFE7L0muK37fwoi+UQQdXMhr9Wr02F3xjSq1rPDnQt742X3WusPH9JdU/bbhK+DtXlpWy6+kU6CAR0mQghKI3yJjVmShvgasLNvuCJNIhqyVIiUh9ji4Y1XfLJHo+NScUdX9/L66B9QSwcIUdbnGf8FAABsDwAAUEsBAhQAFAAIAAgAYW+9QtY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACABhb71CUdbnGf8FAABsDwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAJYGAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
| + | [[Datei:Unten-unten.png|300px]] |
| | |width="1%"| | | |width="1%"| |
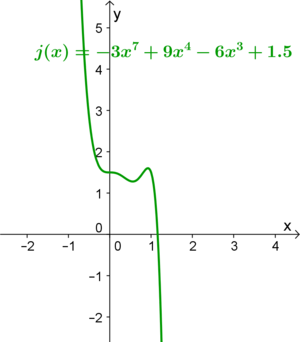
| − | | valign="top"|<big><center>'''<span style="color: #008B00 ">"von links oben nach rechts unten"</span>'''</center><br /> | + | | valign="top"|<big><center>'''<span style="color:#008B00">"von links oben nach rechts unten"</span>'''</center></big><br /> |
| − | <ggb_applet width="363" height="442" version="4.2" ggbBase64="UEsDBBQACAAIAMBtvUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAMBtvUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVdfb9s2EH9OP8VBD0O7xbYo6p87u0VboFiBpCuWbCj2MICSaJmJLGkiZctFXvaZNmDv+yj7JDuSku24SbE2QOPYFMnj3f2Odz9Ss+fdqoA1b6SoyrlDxq4DvEyrTJT53GnVYhQ7z589muW8ynnSMFhUzYqpueOPPWe/DntjP9KLRTZ3Fl7IPBano8WCk5HvhukoWVB3lC6mXpZEIaceSkInxdOyestWXNYs5Rfpkq/YWZUyZXQulaqfTiabzWY8WB9XTT7J82TcycwB9LyUc6d/eIrqbi3aUCPuuS6ZvD8/s+pHopSKlSl3QKNqxbNHJ7ONKLNqAxuRqeXcoVNEtuQiXyLMICQOTLRQjVhrniqx5hKXHnQNZrWqHSPGSj1/Yp+g2MFxIBNrkfFm7rjjgLie67sxCakXBhRtVI3gpeplB5uTQdtsLfjGqtVPxqLvTiPcAiFFUnAMOiskohLlosGIokNNi12ptgVPWDP09/6QU/yggPjAtS7cEBuGuTOdnnre9DRy3dMgcK0rh3YdUFVVGKUuBFO4uQEP4cCpbohtPGzC0E65dsyltvFs49smsDK+Xe5bUd/K+FbGp5+A2ff3OPuBW0AHmPQQJkF8+hvi1+A/whkf4CQaxA0Q7b1pKGi/ifFfN37fDW03Mg1xbUP6yVj/mHiFD0REvwgRObBq0+F+ox+ly85iSP+/Re9BOHcovbtQesE9KB8Y3MEoCQ6Moi3zb74fmaSfhfPe0H6GxdB/SOl/gcHI/RoGZ5OB6GZ97YFcatk+XRVfSc06dGqIBwgEWJhhhDwRAJliE+kC9YAE4AfYJTGEuo2A6pr0gUIMWo5QMPQSxPjjm3oNIUBdejCyhQvUh4ACMaTkA1IRGGJDkvMoSgQBBLhIWyfaLA3BD7FDY/DRQU1pkaYNiuuwj8Y9oASoXksi8EIIPYg0LRJfs2UYa99RqQehC6FeiryInGj5EFfEQDUazPC6kmIX3CUv6t2umDiKsm5VH7t+PF1lQxxVdSSeVen1y6NgcybV8IxCeBjtjzx7ON06EU9mBUt4gfeGC50HAGtW6BI2+hdVqWDIgdiO5Q2rlyKVF1wpXCXhiq3ZGVO8e43ScnDQmDYH9Yy3aSEywcpfMEm0Cq0Qdue2Jqbh3PaJb62kVdVkF1uJmQPdr7yp0AHqjaPAc8OQkCByPRo4sLVTXkzHBzN+jFMyZTrn/el4eviHBbi9ZyoOrW2+3mFjHZdDMPPGXJJs+HXnjXxZFfuhuhKlesVq1TbmFoawGo3qRZkX3ATXECveZ9LrpOoubFSp1XW5rbHnWgeS/FVVVA1gSXoBQsn7NrGtkdGe7aRcI+MaCXfYJpHt5om+G+V9m9jWSOG+W9d6pGSASdzBjJCGSFD5YZaZpJk7nQNtKdSZ7WGGivS6h0rsgrftKsGE69fd1knu1Ln9fJ2zyVGOza55U/LCZlKJe9lWrbSpvUvPk1kr+Tumli/K7CeeY1G+Y5oXFaq2onuXM56KFS60433wmN7Yn9FVO5rxvOEDxMJcfG1ozax7mNcfDRtVr5tq9aZcX2LWHLk6mwx4ZjJtRK2TExIk6mu+z79MSIY0nx2uQ/ASUaSacjCQSgexSng5akvFSwdYq5YVJsj5thFsBWfoByrCYkaQUzhnAskTU1QXcVc3XOrXBrtPMHeukGw6ZKSrx90TmMOIwrfQ/fY4egLfIVebZ/8JjCC0z1SPk7HJ3xkv+AovzqBM3i/a0ri4y4ErcynXew1VcoVkdZQjB5uI80d1QALaVwKwol4yfXPv41ywLW9uRd4o/HGxkFxBN3dGEebYFos3Opg+r7J+u0jPi6Lj2XGO7GtJIT9e4xsAZihWrepL2zz8ILKMl70iTFsbhjviO3cueadIH+Jvfm8r9f0u0N2/f/ytg4ztXzrA3T9/2thauTsijPSsnNuav2qE9yF0PxFCIc/YJX9/PGyOIckbsdjdWZA8z/v3Xns8uf1FZrdH+L7YqHeak8FsLBnHlHh0GoZT3yN+rKlwq1+BIzyB9h/csA9W8dEGTQ5ryRxu/dvts/8AUEsHCGurxeEGBgAAjQ8AAFBLAQIUABQACAAIAMBtvULWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAwG29QmurxeEGBgAAjQ8AAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACdBgAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /> | + | [[Datei:Oben-unten.png|300px]] |
| | + | |} |
| | + | |
| | + | </popup> |
| | + | </td></tr></table></center> |
| | + | </div> |
| | + | |
| | + | <div style="padding:1px;background:#66CD00;border:0px groove;"> |
| | + | |
| | + | |
| | + | <center><table border="0" width="850px" cellpadding=5 cellspacing=15> |
| | + | <tr><td width="800px" valign="top"> |
| | + | === <big>Übung === |
| | + | Teste dein Wissen mit dieser Aufgabe aus dem Känguru-Wettbewerb 2013:</big><br /> |
| | + | <br /> |
| | + | <iframe src="http://LearningApps.org/watch?v=pfiz98zzc" style="border:0px;width:100%;height:1160px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
| | + | <br /> |
| | + | |
| | + | <popup name="Lösung"> |
| | + | W(x) = (a - x) (b - x)<sup>2</sup><br /> |
| | + | <br /> |
| | + | Die Funktion hat eine einfache Nullstelle bei a (der Graph schneidet die x- Achse) und eine doppelte Nullstelle bei b (der Graph berührt die x- Achse).<br /> |
| | + | -> mögliche Lösungen: A, B, C, D<br /> |
| | + | <br /> |
| | + | Da a < b ist, muss die einfache Nullstelle vor der doppelten liegen.<br /> |
| | + | -> mögliche Lösungen: A, D<br /> |
| | + | <br /> |
| | + | Ausmultiplizieren des Funktionsterms ergibt W(x) = - x<sup>3</sup> +...<br /> |
| | + | W(x) hat den Leitkoeffizienten: -1.<br /> |
| | + | Damit verläuft die Funktion von links oben nach rechts unten.<br /> |
| | + | -> Lösung: A |
| | + | |
| | + | </popup> |
| | + | |
| | + | </td></tr></table></center> |
| | + | </div> |
| | + | <br /> |
| | + | <br /> |
| | + | |
| | + | {| |
| | + | {{Vorlage:Lesepfad Ende |
| | + | |Link zurück=[[Manipulationen an Funktionen/Grenzwerte im Unendlichen|Zurück zu den Grenzwerten im Unendlichen]] |
| | + | |Link vor= |
| | + | |Text Copyright=<colorize>Manipulationen an Funktionen</colorize> |
| | + | }} |
| | |} | | |} |