Achtung:

Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.

Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.

Gerne kannst Du natürlich weiterarbeiten

im neuen Projektwiki (projekte.zum.de).

Wiederholung:Ganzrationale Funktionen: Unterschied zwischen den Versionen

Aus Projektwiki - ein Wiki mit Schülern für Schüler.
Wechseln zu: Navigation, Suche
K
 
(6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
__NOTOC__
 +
<div style="padding:1px;background:#66CD00;border:0px groove;">
 +
 +
 +
<center><table border="0" width="850px" cellpadding=5 cellspacing=15>
 +
<tr><td  width="800px" valign="top">
 +
<big>Der charakteristische Verlauf von ganzrationalen Funktionen ist von zwei Faktoren abhängig. Worauf es genau ankommt, kannst du im folgenden Applet mit den Schiebereglern untersuchen.<br />
 +
Welche '''vier Fälle''' unterscheidet man?</big>
 +
<br />
 +
<center>
 +
<ggb_applet width="585" height="489"  version="4.2" ggbBase64="UEsDBBQACAAIAPmLEEMAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAD5ixBDAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbM1Y62/bNhD/nP4VB30Y2i2xRVEvd3aLrkCxAklXLFnRbdgAWqJtNrKkiZQfRf/4HR+yZSfN1mQolsTmQ8e7+92Lp4yfb5YFrHgjRVVOPDLwPeBlVuWinE+8Vs3OUu/5s0fjOa/mfNowmFXNkqmJFw4Cb38OVwMa68Min3jJNPTzjORnAefsLAxJdjYKkuCMxFkcBCQM83TmAWykeFpWb9iSy5pl/DJb8CU7rzKmDM+FUvXT4XC9Xg866YOqmQ/n8+lgI3MPUPNSTjw3eYrsDg6tqSEPfJ8M31+cW/ZnopSKlRn3QKNqxbNHJ+O1KPNqDWuRq8XEiwkiW3AxXyDM2EdMQ01UI9aaZ0qsuMSjvaXBrJa1Z8hYqZ+f2BkUOzge5GIlct5MPH9AgzgZJTSN4sAfkcgPPagawUvliIkTOuzYjVeCry1fPTMiQ3+UoA+EFNOCT7wZKyTCEuWsQZOiRk2LS6m2BZ+yplvvFSKn+IsE4iPXvBCntcPEo5SepqPTxPdPo8jh78v1QFVVYZj6EI3g0ycI/MCHUz0QOwQ4xLF95Ns9n9ohsENoh8jShPZ4aElDSxNampDeAdOt9zjdxgHQDibtwySIT3/Qx6ehfxNn2sNJNIhPQLT2ZqCg9SZGfz2EbhnbZWIG4tuBuIep/jL2ih+IiN4LEelJteHweaE3wqWTGKXRv5cYPAjnDmVwG8og+gzKBxq3E0qinlCUZf7M54ZI+kU4P2vaL5AYhw9J/XsITPyDtO9y3o7EjXeZ4T9TajzsiuHYKQRyoWldSCu+lFpFOjLFCQhEmLxxgrUkAjLCIdFJHACJIIxwSVKI9ZgA1XkbAoUUNB2hYEpQlOJXaHI6hgh56c3EJjfQECIKxBSuENAKYIof2iSgSBFFEOEhLZ1osTSGMMYFTSFEBXXZS3RpoXgO1yg8AEqA6rMkgSCGOIBEl04S6ooap1p3ZBpA7EOsj2LtxLppayaeSIFqNJgFdSXFzrgLXtQ7rxg7irJulbOd28+WeWdHVR2R51V2/cORsTmTqpsjEV5Y+3vRXmAH1+bJuGBTXmBzcanjAGDFCp3mhv+sKhV0MRDbvXnD6oXI5CVXCk9J+MBW7JwpvnmF1LJT0Ig2t/mYt1khcsHKdxgkmoVmCN3lbopXd7mHMbFSsqpq8sutxMiBzW+8qbDiBMFg1P9BC27dIxoM/P4PWlpmTMd8ODo8hPfz1j2K/MNDTjRf7aCxDZedLeeNyPvz1/KHqsh3/qgrUaqXrFZtYxo1LJSNxvSinBfcmNaUXmx5sutptbm0NqWW19W2xpVv5U/nL6uiagATMojQNnM3Tu1oaLRiOyrf0PiGwu+cJPLdczIKDIUZp3Y0VOh1q5oDSjqUxO/ECGlKDTLvx5gJmYm38aAthTq3K4xPkV07qMQeeNMupxhu7twhT3Irz+19eGqtsZmT6r1rmPX81978asEV021eFNBolCZJhN/BKE1tnB5F6PiaNyUvbByWGApt1UqbGLvgPhm3kr9lavGizH/mc0zpt0xXVYWqWdK9ejnPxBIP2n1nfKYD4xeEandzPm94Z6LC9NbWNeap38+KG9uG1aumWr4uV1cYdUeqjocdnrHMGlHr2IYplvlrvo9ftBLDSyLvn0PwElFkumChI5R2wssFwrxGlGhVITGcG3jHm4K1+P7AWrWoMOAuto1gSzhHvZAxlgZdPeBFO2+lwmqMUa+rQsGX2F6DMrFftktkme3CgJnWHXG0Dqp2pQGrQwCq6QesYEehszc4Pv5MdgAr6oWJBJftBdsihL41DbeLKu8EO7GFflOApcDSfYbZuGQbrCDIbyqrolX4roTuK/fvSlYzV+OwN9KRiCdoQvVsi71soCczseG7soLGEx8x4A6jZ5+lCuvuNb59SFNKlCsaZvKjyHNe7rRlJQaccRtW0NqQY83nNut2B2sEb4pVL1ScW/7RQdNjB8X/IwcR5x/iP8BBhH5ND5H7eGhTNyhLM3EWxiTETRwfb57ABBh8C5s/H0+fwHdmhDMgT2xbcOjdWVuaLPf2jO52Za8O9n3ZXVg3venf6c2fZjPJlbZ/lBrjdxfd7b6+1eDRXQa/22xXfKOIM903f7WV+t4Z0C7Qeo/P2RV///vsD21Ku2u/b7Mm9kLKO+T9Va25t5fbNTF8fCsJaTAdb5ueT2Kuz3YvCNirXLjL1PaCvntr2CefYo16q1sg0E7ERs26kQyi8KDHwvbr466Y950y7F82pnd0/2F69jdQSwcI6qlu55oGAAAREwAAUEsBAhQAFAAIAAgA+YsQQ0XM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAD5ixBD6qlu55oGAAAREwAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAADIHAAAAAA==" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" useLocalJar="true" />
 +
</center>
 +
<br />
 +
<popup name="Lösung">
 
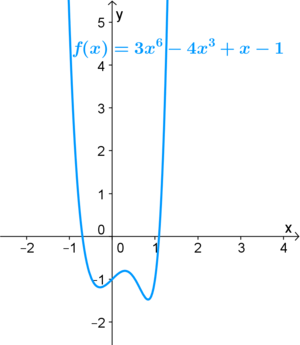
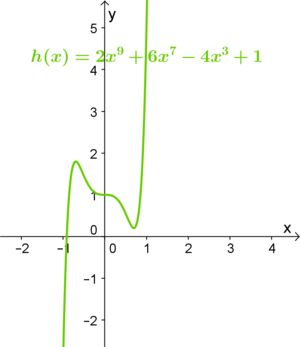
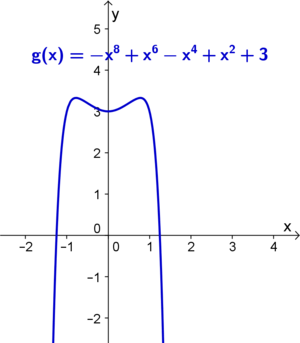
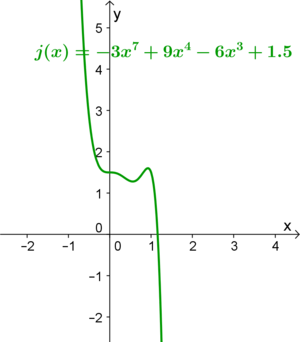
Bei ganzrationalen Funktionen ist der '''Grad der Funktion''', sowie das '''Vorzeichen des Leitkoeffizienten''' dafür ausschlaggebend, zu welchem der vier charakteristischen Verläufe die Funktion gehört:<br />
 
Bei ganzrationalen Funktionen ist der '''Grad der Funktion''', sowie das '''Vorzeichen des Leitkoeffizienten''' dafür ausschlaggebend, zu welchem der vier charakteristischen Verläufe die Funktion gehört:<br />
 +
<br />
  
 
{|
 
{|
−
| valign="top"|<big><center>'''<span style="color: #00BFFF ">"von links oben nach rechts oben"</span>'''</center><br />
+
| valign="top"|<big><center>'''<span style="color:#00BFFF">"von links oben nach rechts oben"</span>'''</center></big><br />
 
[[Datei:Oben-oben.png|300px]]
 
[[Datei:Oben-oben.png|300px]]
 
|width="1%"|
 
|width="1%"|
−
| valign="top"|<big><center>'''<span style="color: #9ACD32 ">"von links unten nach rechts oben"</span>'''</center><br />
+
| valign="top"|<big><center>'''<span style="color:#9ACD32">"von links unten nach rechts oben"</span>'''</center></big><br />
 
[[Datei:Unten-oben.png|300px]]
 
[[Datei:Unten-oben.png|300px]]
 
|-
 
|-
 
| <br>
 
| <br>
 
|-
 
|-
−
| valign="top"|<big><center>'''<span style="color: #0000CD ">"von links unten nach rechts unten"</span>'''</center><br />
+
| valign="top"|<big><center>'''<span style="color:#0000CD">"von links unten nach rechts unten"</span>'''</center></big><br />
 
[[Datei:Unten-unten.png|300px]]
 
[[Datei:Unten-unten.png|300px]]
 
|width="1%"|
 
|width="1%"|
−
| valign="top"|<big><center>'''<span style="color: #008B00 ">"von links oben nach rechts unten"</span>'''</center><br />
+
| valign="top"|<big><center>'''<span style="color:#008B00">"von links oben nach rechts unten"</span>'''</center></big><br />
 
[[Datei:Oben-unten.png|300px]]
 
[[Datei:Oben-unten.png|300px]]
 
|}
 
|}
  
 +
</popup>
 +
</td></tr></table></center>
 +
</div>
 +
 +
<div style="padding:1px;background:#66CD00;border:0px groove;">
 +
 +
 +
<center><table border="0" width="850px" cellpadding=5 cellspacing=15>
 +
<tr><td  width="800px" valign="top">
 +
=== <big>Übung ===
 +
Teste dein Wissen mit dieser Aufgabe aus dem Känguru-Wettbewerb 2013:</big><br />
 
<br />
 
<br />
−
<br />
+
<iframe src="http://LearningApps.org/watch?v=pfiz98zzc" style="border:0px;width:100%;height:1160px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
−
Teste dein Wissen mit dieser Aufgabe aus dem Känguru-Wettbewerb 2013:<br />
+
−
<br />
+
−
<iframe src="http://LearningApps.org/watch?v=pfiz98zzc" style="border:0px;width:100%;height:1100px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
+
 
<br />
 
<br />
  
−
<popup name="Lösung">
+
<popup name="Lösung">
 +
W(x) = (a - x) (b - x)<sup>2</sup><br />
 +
<br />
 
Die Funktion hat eine einfache Nullstelle bei a (der Graph schneidet die x- Achse) und eine doppelte Nullstelle bei b (der Graph berührt die x- Achse).<br />
 
Die Funktion hat eine einfache Nullstelle bei a (der Graph schneidet die x- Achse) und eine doppelte Nullstelle bei b (der Graph berührt die x- Achse).<br />
 
-> mögliche Lösungen: A, B, C, D<br />
 
-> mögliche Lösungen: A, B, C, D<br />
Zeile 38: Zeile 63:
 
</popup>
 
</popup>
  
 +
</td></tr></table></center>
 +
</div>
 
<br />
 
<br />
 
<br />
 
<br />
  
 +
{|
 
{{Vorlage:Lesepfad Ende
 
{{Vorlage:Lesepfad Ende
 
|Link zurück=[[Manipulationen an Funktionen/Grenzwerte im Unendlichen|Zurück zu den Grenzwerten im Unendlichen]]
 
|Link zurück=[[Manipulationen an Funktionen/Grenzwerte im Unendlichen|Zurück zu den Grenzwerten im Unendlichen]]
 
|Link vor=
 
|Link vor=
−
|Text Copyright=Manipulationen an Funktionen
+
|Text Copyright=<colorize>Manipulationen an Funktionen</colorize>
 
}}
 
}}
 +
|}

Aktuelle Version vom 16. August 2013, 16:32 Uhr


Der charakteristische Verlauf von ganzrationalen Funktionen ist von zwei Faktoren abhängig. Worauf es genau ankommt, kannst du im folgenden Applet mit den Schiebereglern untersuchen.
Welche vier Fälle unterscheidet man?



Übung

Teste dein Wissen mit dieser Aufgabe aus dem Känguru-Wettbewerb 2013:




Zurück zu den Grenzwerten im Unendlichen

Manipulationen an Funktionen

Von „https://projektwiki.zum.de/index.php?title=Manipulationen_an_Funktionen/Grenzwerte_im_Unendlichen/Wiederholung:Ganzrationale_Funktionen&oldid=3511“