Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Punktsymmetrie zum Ursprung: Unterschied zwischen den Versionen
(→Übung) |
K |
||
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
<center><table border="0" width="800px" cellpadding=5 cellspacing=15> | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | + | <big>Spiegle die Punkte '''<span style="color:#008B00 ">A</span>''', '''<span style="color: #008B00 ">B</span>''', '''<span style="color: #008B00 ">C</span>''', '''<span style="color: #008B00 ">D</span>''' und '''<span style="color: #008B00 ">E</span>''' im Applet am '''<span style="color: #551A8B">Koordinatenursprung</span>''':<br /> | |
| − | + | ||
<br /> | <br /> | ||
Achte dabei auf die Kooordinaten der Spiegelpunkte.<br /> | Achte dabei auf die Kooordinaten der Spiegelpunkte.<br /> | ||
| Zeile 13: | Zeile 12: | ||
<br /> | <br /> | ||
Verbinde die Punkte zu einem Funktionsgraphen.<br /> | Verbinde die Punkte zu einem Funktionsgraphen.<br /> | ||
| − | Um welche Funktion handelt es sich hier?<br /> | + | Um welche Funktion handelt es sich hier?<br /></big> |
<br /> | <br /> | ||
| − | + | {| | |
| − | <popup name="Hilfe zu GeoGebra"> | + | | valign=top width="400"|<popup name="Hilfe zu GeoGebra"> |
*Auch für die Punktspiegelung gibt es ein Symbol in der Werkzeugleiste: "Spiegle Objekt an Punkt" | *Auch für die Punktspiegelung gibt es ein Symbol in der Werkzeugleiste: "Spiegle Objekt an Punkt" | ||
**Du kannst es unter dem Symbol für Achsenspiegelung auswählen. | **Du kannst es unter dem Symbol für Achsenspiegelung auswählen. | ||
| Zeile 25: | Zeile 24: | ||
|width="0,5%"| | |width="0,5%"| | ||
| − | |<ggb_applet width="580" height="797" version="4.2" ggbBase64="UEsDBBQACAAIADlMvUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIADlMvUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VhZc9s2EH52fsUOny0JB8+MlIyTtjOZsdNMnXTSvkEkRCHmNSR0ZfLjuwBISZZz1HbSTB1LOLjYxffh2wWd6fNtWcBatp2qq5lHx8QDWaV1pqp85q30YhR7z589meayzuW8FbCo21LomeePmXdYh6OxH5nFKpt5fLGgYSyCUSCiYOQTGoziVMxHLImCOQ0XNJbCA9h26mlVvxal7BqRyut0KUtxWadCW59LrZunk8lmsxkP0cd1m0/yfD7edpkHuPOqm3l95ym6u7Vow605I4RO3l9dOvcjVXVaVKn0wKBaqWdPzqYbVWX1BjYq08uZF5LEg6VU+RJhxmHowcQYNYi1kalWa9nh0qOhxazLxrNmojLPz1wPij0cDzK1VplsZx4Zcxb7JGLMT4I48RPqQd0qWenelvYxJ4O36VrJjXNrejaiT5IIj0B1al7ImbcQRYeoVLVokVHcULvCYad3hZyLdhgf9kPP8R8aqI/S+MKjczQgASE/x62dR4ScBwFxezkO7IGu68J6JRAk8OkTMMIInJuGuoZhE4buEXFzhLuGucZ3TeBsfLfcd6a+s/Gdjc+/grMfH4D2E7eQDjj5MU6K+MwnxI8l4ARnfISTGhCfgJrd24aD2Te1+zeN3w9DN4xsQ4lraP8wNl+Wr/CRiPiDENGjqE4PXw56Ry9DxCC+R0T2KJx7lOxzKFnwBZSPJHcISoOjoBjL/trPnZD8Xji/SO09Iob+Y3L/AQEj8l8EnE6GSjftcw+6pbHt5apl2ZmqwxNbeIBCgIkZRlgnAqAJNpFJUAY0AD/AIY0hNG0E3OSkDxxiMHaUgy0vQYxfvs3XEAL0ZSYjl7jAfQg4UFuUfMBSBLawYZFjHC2CAAJcZKJTE5aH4Ic44DH4uEFT0iJTNjiuwzEGZ8ApcLOWRsBCCBlEpixS31TLMDZ7R6cMQgKhWYp1EWuiq4e4IgZu0KDCm7pTe3KXsmj2p2J5VFWz0j13/XxaZgOPuj4xz+r05sUJ2VJ0euijEd5GhzvP3U63rsSzaSHmssAXh2ujA4C1KEwKW/+LutIwaCB2c3krmqVKu2upNa7q4INYi0uh5fY3tO6GDdrQ9qaeylVaqEyJ6k8UiXFhHMJwcdvCNFzcEU1clLSu2+x616FyYPu3bGusJhEZMx/vmpiRAG94Gniwc494xMcR8yl+QvwKI7xiu1QYzUfhOCFh7PPIT8wPnsHuziMUMt4UoQst13toYiu7gcu8Vdlx/1X3oi6y/Xk0tar0S9HoVWtfwrAItgbTRZUX0lJryyq+zqQ383p77TjlztfbXYMj4uLP85d1UbeACckCxJj37dy11sZsbG9FrA2xFmQ4JJXtn9OEWQvbzl1rrfDU3dZ6oHRASckQRnW2jKDzY41Zycy8rQerSulLN0J9qvSmh0rdgterco5y69fd9kk/63P3EJ9m1/ii1un35jUt8Gz/r6P+26XUwo4ZD5I4igL8ZkkcO52eKHR6I9tKFk6HFUphVa86lxh7cZ9NV518I/Tyosr+kDmm9BthqqrGrTnTw/YymaoSF7p5v+fBCOMdQnWzmcxbOVBU2PdmdzT2KTnOijvT1tVvbV2+qtZvUXUnW51OBjzTLm1VY7QNcyzzN/KgX2RJ4CWRHa9D8B2iSE3BwoPQ5hDerKob3TVK5rJYoR9VwjusJy32PRArvaxRcVe7VokSLoWZzLA2oHQTuBIKazFq3rouS1FlUNmL6FVlaMOa5B2KoCAosAsUC7qlqAvbtXDrlR4MLhy+3pupNYUs8Y0ctM0om5R7aV1Y70ZCUM8/YLQT6R0ODB8fsofFR/llR6JollZNPf+F2Mn21olYj78vFp3UsLX5BLtDWtmnV3XWnyLti63ayuxUOvbEO+PDRDNORrbz0f3V5/7GMShNQXGLo+PZE62g1B1B36DqxYOocoWIkqEU3Z+oEU8sSBY9gqmRTfueqpAFX2WLfwe2Xv4stiLfsZU8hi16ENaPp+qX/zlVvbDoOIyjH8/Wrz8tDfl3SEM2CMv/RsX6t1RNji8k+37Z/w/Ts38AUEsHCAw2aLcDBgAAERMAAFBLAQIUABQACAAIADlMvULWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAOUy9Qgw2aLcDBgAAERMAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACaBgAAAAA=" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /> | + | |<ggb_applet width="580" height="797" version="4.2" ggbBase64="UEsDBBQACAAIADlMvUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIADlMvUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VhZc9s2EH52fsUOny0JB8+MlIyTtjOZsdNMnXTSvkEkRCHmNSR0ZfLjuwBISZZz1HbSTB1LOLjYxffh2wWd6fNtWcBatp2qq5lHx8QDWaV1pqp85q30YhR7z589meayzuW8FbCo21LomeePmXdYh6OxH5nFKpt5fLGgYSyCUSCiYOQTGoziVMxHLImCOQ0XNJbCA9h26mlVvxal7BqRyut0KUtxWadCW59LrZunk8lmsxkP0cd1m0/yfD7edpkHuPOqm3l95ym6u7Vow605I4RO3l9dOvcjVXVaVKn0wKBaqWdPzqYbVWX1BjYq08uZF5LEg6VU+RJhxmHowcQYNYi1kalWa9nh0qOhxazLxrNmojLPz1wPij0cDzK1VplsZx4Zcxb7JGLMT4I48RPqQd0qWenelvYxJ4O36VrJjXNrejaiT5IIj0B1al7ImbcQRYeoVLVokVHcULvCYad3hZyLdhgf9kPP8R8aqI/S+MKjczQgASE/x62dR4ScBwFxezkO7IGu68J6JRAk8OkTMMIInJuGuoZhE4buEXFzhLuGucZ3TeBsfLfcd6a+s/Gdjc+/grMfH4D2E7eQDjj5MU6K+MwnxI8l4ARnfISTGhCfgJrd24aD2Te1+zeN3w9DN4xsQ4lraP8wNl+Wr/CRiPiDENGjqE4PXw56Ry9DxCC+R0T2KJx7lOxzKFnwBZSPJHcISoOjoBjL/trPnZD8Xji/SO09Iob+Y3L/AQEj8l8EnE6GSjftcw+6pbHt5apl2ZmqwxNbeIBCgIkZRlgnAqAJNpFJUAY0AD/AIY0hNG0E3OSkDxxiMHaUgy0vQYxfvs3XEAL0ZSYjl7jAfQg4UFuUfMBSBLawYZFjHC2CAAJcZKJTE5aH4Ic44DH4uEFT0iJTNjiuwzEGZ8ApcLOWRsBCCBlEpixS31TLMDZ7R6cMQgKhWYp1EWuiq4e4IgZu0KDCm7pTe3KXsmj2p2J5VFWz0j13/XxaZgOPuj4xz+r05sUJ2VJ0euijEd5GhzvP3U63rsSzaSHmssAXh2ujA4C1KEwKW/+LutIwaCB2c3krmqVKu2upNa7q4INYi0uh5fY3tO6GDdrQ9qaeylVaqEyJ6k8UiXFhHMJwcdvCNFzcEU1clLSu2+x616FyYPu3bGusJhEZMx/vmpiRAG94Gniwc494xMcR8yl+QvwKI7xiu1QYzUfhOCFh7PPIT8wPnsHuziMUMt4UoQst13toYiu7gcu8Vdlx/1X3oi6y/Xk0tar0S9HoVWtfwrAItgbTRZUX0lJryyq+zqQ383p77TjlztfbXYMj4uLP85d1UbeACckCxJj37dy11sZsbG9FrA2xFmQ4JJXtn9OEWQvbzl1rrfDU3dZ6oHRASckQRnW2jKDzY41Zycy8rQerSulLN0J9qvSmh0rdgterco5y69fd9kk/63P3EJ9m1/ii1un35jUt8Gz/r6P+26XUwo4ZD5I4igL8ZkkcO52eKHR6I9tKFk6HFUphVa86lxh7cZ9NV518I/Tyosr+kDmm9BthqqrGrTnTw/YymaoSF7p5v+fBCOMdQnWzmcxbOVBU2PdmdzT2KTnOijvT1tVvbV2+qtZvUXUnW51OBjzTLm1VY7QNcyzzN/KgX2RJ4CWRHa9D8B2iSE3BwoPQ5hDerKob3TVK5rJYoR9VwjusJy32PRArvaxRcVe7VokSLoWZzLA2oHQTuBIKazFq3rouS1FlUNmL6FVlaMOa5B2KoCAosAsUC7qlqAvbtXDrlR4MLhy+3pupNYUs8Y0ctM0om5R7aV1Y70ZCUM8/YLQT6R0ODB8fsofFR/llR6JollZNPf+F2Mn21olYj78vFp3UsLX5BLtDWtmnV3XWnyLti63ayuxUOvbEO+PDRDNORrbz0f3V5/7GMShNQXGLo+PZE62g1B1B36DqxYOocoWIkqEU3Z+oEU8sSBY9gqmRTfueqpAFX2WLfwe2Xv4stiLfsZU8hi16ENaPp+qX/zlVvbDoOIyjH8/Wrz8tDfl3SEM2CMv/RsX6t1RNji8k+37Z/w/Ts38AUEsHCAw2aLcDBgAAERMAAFBLAQIUABQACAAIADlMvULWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAOUy9Qgw2aLcDBgAAERMAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACaBgAAAAA=" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" useLocalJar="true"/> |
| + | |} | ||
<br /> | <br /> | ||
| − | < | + | <big>Zeichne den so entstandenen Funktionsgraphen auf deinem Arbeitsblatt ein und fülle die Lücken dort aus, nachdem du die Antworten mit dem folgenden Lückentext kontrolliert hast.</big><br /> |
| − | + | <iframe src="http://LearningApps.org/watch?v=pq4kbmcq5" style="border:0px;width:100%;height:590px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | </ | + | |
| − | + | ||
</td></tr></table></center> | </td></tr></table></center> | ||
</div> | </div> | ||
| Zeile 44: | Zeile 38: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | === <big>Allgemein</big> | + | === <big>Allgemein === |
| + | |||
| + | Wie lässt sich diese Feststellung verallgemeinern?<br /> | ||
| + | Setze die richtigen Lücken ein und übertrage sie anschließend auf dein Arbeitsblatt.<br /></big> | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 59: | Zeile 56: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | <big>Welche weiteren Funktionen kennst du, deren Graph punktsymmetrisch zum '''<span style="color: #551A8B ">Ursprung</span>''' | + | <big>Welche weiteren Funktionen kennst du, deren Graph punktsymmetrisch zum '''<span style="color: #551A8B ">Ursprung</span>''' verläuft?<br /> |
Überlege dir, wie der Graph einer solchen Funktion aussehen muss und worauf es im Funktionsterm ankommt.<br /> | Überlege dir, wie der Graph einer solchen Funktion aussehen muss und worauf es im Funktionsterm ankommt.<br /> | ||
<br /> | <br /> | ||
| Zeile 65: | Zeile 62: | ||
Stelle sie so ein, dass '''f''' '''<span style="color: #551A8B ">punktsymmetrisch zum Ursprung</span>''' verläuft.<br /> | Stelle sie so ein, dass '''f''' '''<span style="color: #551A8B ">punktsymmetrisch zum Ursprung</span>''' verläuft.<br /> | ||
</big> | </big> | ||
| − | + | <center><ggb_applet width="580" height="463" version="4.2" ggbBase64="UEsDBBQACAAIAJulx0IAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACACbpcdCAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbOVa647buBX+PfsUhH4USXfGFkVRslM7i0mAxaaYbINOtli0aABaom3u6OKVqBk5yAv0KfpufZIeXiRbtsdjx7PNpDuJTZHi7XzfOR9JyaPv6jRBt7woRZ6NHdxzHcSzKI9FNhs7lZxeDJzvXn4zmvF8xicFQ9O8SJkcO37Pc1btINfzQ9VYxGOHBhzHzA0vSIzjCz+MyAXjZHAxHMQ0HhIaYD92EKpL8SLLf2QpLxcs4tfRnKfsKo+Y1H3OpVy86Pfv7u56zei9vJj1Z7NJry6hA5h5Vo4de/ECuus0uiO6uue6uP/z2yvT/YXISsmyiDtIWVWJl9+cje5EFud36E7Ecg6zHw4dNOdiNgczaeg7qK8qLcDWBY+kuOUlNF3LaptlunB0NZap+2fmCiWtOQ6Kxa2IeTF23B4OqTf0MCV0MCSYUsAyLwTPpK2M7aD9prvRreB3pl91pYf03WEIHIhSTBI+dqYsKcEskU0LgBRmVFSQLeUy4RNWNPnVhPA5/IMK4iNXfQF3Bgcwmg7OsUvOQ9c9p9Q1c1kf2EEyzxPdq4voEH36hDzXc9G5SrBJPEiCwNxyTZlLTOKZxDcJNXV809w3VX1Txzd1fLLHTptfGWoLOpY2dpJ1OzHYpz4BfDQAG3YO1uzEyohPCKvZ64QgNW+s568S32YDkw11gl2TYHtzoL40XsGJFpHPsgivjWr84f5Bt/ylGZEOjhjRO8nO1krs0u0xPXqPlSeC2w5K14MCYkH915+tIclRdt4L7REjBv4psf8ZA4ZuJ+ybmDcptuk+GB5tUqN+o4YjOyFUzlVd69KSp6WaIhlqcUIYUQjeIAQtoQgPIQlVEHsIU+RTyOIBClQaIqLi1kcEDZCqhwnSEkQH8OXrmA4Qhb5UYWiCGxEfUYKwFi4fAQpIix9g4hGoQSmi0EiNjtWwJEB+ABkyQD5MUMleqKSFQDvIw+AeIhgR1RaHyAtQ4KFQSSf2laIGAzV36NRDgYsC1RS0E3TTaCa0GCCirIEoWOSlaMGd82TRsqJxFNmikhY7Wx6lcYOjzDeqx3l082oDbM5K2VxDJVixVgujWcE66+bZKGETnsDu4lr5AUK3LFFhrvuf5plEjQ8EpmxWsMVcROU1lxJalegXdsuumOT191C7bCaoh9bL+YhXUSJiwbK/gZOoLlSHqF3dlXg1q7tPqBklyvMivl6W4Dmo/jsvcpjAAPYz63+gRUtzi2C91SkjptzcH/aG63+waizvuWUG47etMazmZYPerBDx+vWb8lWexC0Di1xk8jVbyKrQezOYTqGsuMxmCddgarGFXU50M8nra4MiMX29Xy4g55rxJ7PXeZIXCELQoyCrM5tOTKrrqIm1tVxdx9U13IYWEbf38dDTNXQ6MamuBTybqVlDcWMldpthRKnFRcG55lXaScZO7aAqE/LK5MAjRXRjTcWmwY9VOgEHs+26feKdfS6P73PU3/Cp0Q0vMp4Yz8mAyiqvSuPKrTuejaqSv2NyfpnFf+UzCMJ3TOmghK5N1dWUYx6JFBqacgseU8T+BFM1pTGfFbwxMdHbYQOtvuuu+/FWse7q+yJP32S378FrNqY66jf2jMqoEAvlm2gCwnzDV/4Xi5KBrMfr7cD4EqyIlMQAkFKB+K7KbmS5TMFS2NGij1WKfgIFKKps5iBWyXkOHvN2WQiWoiumCmOIZlhe0J+BF1BP8FkVxQlPYT+MpPbcrEp5IaKWRK732mBFZQ1VBxdtqiIQ5ZNfQHE2iF/BDbe3IoBiEwAuLKssWcyZ3qZbN2ZLXnQA1V2+zeNmdDt2ovb3KBWZduiU1dqn2KTMk0rCAQcIzFYHHDM7q0vEVZJSK82g6moJcwn0cWwqat4KA6AnPoLLdf1nFWcStPIGjgylFgNpw15f/CDimGftZFkGLqeJA9VbGOdfcG7ipm24ANu13Kw5i6XmQZLiRycJe6EVoS/MkTnrKo48+lVzFD0aR2aR0PHzBBgiw/D/JIomj8wQpqRd6r8wR/6gjaLwq+aIPZ7SeU0caZKCLx1H3te0GtWLAsZSnViMp3A+qdUh5ln9HI3RM4b+iOrnH575z9G36NnE5ojORTbnqVysMpDaQ02X/WmV6R2Psxrm88PR3ZJL90CabakmZHNDuZMCuo+C/UC+57XEFsw//Frl8k8WUpNR+F2x9/znf0z/qeAzpeZ7F4JwepNOt+/9CK7tqv9XEIpSW7RZrM+oJUT/tH2gASettyrk/eb5RWifcqxCUbJCvlMHOKSC6sLr+Z2jJQ51iF3gHsT/2p8PXX5s1eRhirwORaj+4FsODqDAO5wC2PbHwgQrVP+Lrc3Qf/71b4SP07QnzpTXI76mxu2F3YcBwXHMkA4z3wI15HBqyKnUTO6jZt+W4IlTQ3ou7TxcCRqicKeYHEeU3yWq/uAdzpN/Kk/Rfp52ba6fOEv+BksDS1LQ4Ugdvo8hiW5G0+Ec0VM5iu+VuT2H1CfOEu3hjrqply2aJhp2ePKOoynYoAkfTlNwKk38IZp2PvB54jwFPbdRua72DY8MoHDHXu5wcsLf1W4NsCYdCRs2GuYftiOI8jRlWYwy/RZMd6wBNG9fmDt2lpe1KC1glWxKL01HtvkWLfqFQIv55TYnzYvNfYcQ7DWiRU/fAmwe4tSRdesYh3cd4+yT69LgbQ6cgUpXiJ6NtMHqvUbnpZEp3Xjk/RjwvzoG/ldPEP5TwKe/CfhXcCzdwP4S7MUW7A78s/3wqxNuC+7sIfTvUSTsemuadNJSsIIQWwhdC+Gqq12Hcn//cxH+a2aaWIkS6SIRkZCPh/P8CJznv3ucdy+ng85yujx8JR18eUDXl8jmhyrNGuk2a6T74BrpdneKfmBlZLi+SOJ7N5Bd/32TqbekAMeGE9daqLUj79bs18do9uvP28b8Js7c6O6F+4DwBgcKb3/93az+cYT9DeXL/wJQSwcI1EdJaKQIAADzKQAAUEsBAhQAFAAIAAgAm6XHQkXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACACbpcdC1EdJaKQIAADzKQAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAADwJAAAAAA==" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" useLocalJar="true"/></center> | |
<br /> | <br /> | ||
| − | |||
<br /> | <br /> | ||
| + | |||
| + | <big>Kannst du die Lücken der Definition auf deinem Arbeitsblatt schon ausfüllen?<br /> | ||
| + | Kontrolliere dich mit der folgenden Lösung:<br /></big> | ||
<br /> | <br /> | ||
| − | <popup name="Lösung"> | + | <popup name="Lösung und Definition"> |
{| | {| | ||
| valign="top"| | | valign="top"| | ||
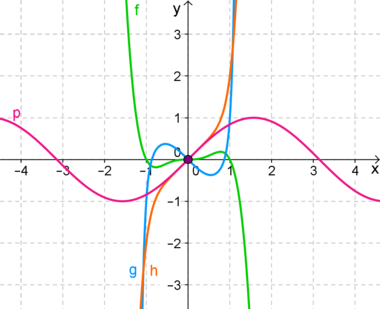
| − | Beispiele für zum '''<span style="color: #551A8B ">Ursprung</span>''' | + | Beispiele für Funktionsgleichungen zum '''<span style="color: #551A8B ">Ursprung</span>''' punktsymmetrischer Funktionen sind: <br /> |
*'''<span style="color: #00CD00 ">f (x) = -x<sup>5</sup> + x<sup>3</sup></span>'''<br /> | *'''<span style="color: #00CD00 ">f (x) = -x<sup>5</sup> + x<sup>3</sup></span>'''<br /> | ||
*'''<span style="color: #00C5CD ">g(x) = x<sup>15</sup> - x<sup>9</sup> + x<sup>7</sup> + x<sup>3</sup> - x</span>'''<br /> | *'''<span style="color: #00C5CD ">g(x) = x<sup>15</sup> - x<sup>9</sup> + x<sup>7</sup> + x<sup>3</sup> - x</span>'''<br /> | ||
*'''<span style="color: #EE7600 ">h(x) = x<sup>7</sup> + x</span>'''<br /> | *'''<span style="color: #EE7600 ">h(x) = x<sup>7</sup> + x</span>'''<br /> | ||
| − | *'''<span style="color: # | + | *'''<span style="color: #EE1289 ">p(x) = sin(x)</span>'''<br /> |
| − | Bei den ganzrationalen Funktionen dürfen <span style="color: red">nur | + | Bei den ganzrationalen Funktionen dürfen <span style="color: red">nur x- Potenzen mit <u>ungeraden</u> Exponenten</span> im Funktionsterm auftauchen, also x<sup>1</sup>, x<sup>3</sup>, x<sup>5</sup>, ...<br /> |
<br /> | <br /> | ||
| − | Eine Funktion, die nur ungerade Exponenten enthält, nennt man<br /> | + | Eine ganzrationale Funktion, die nur ungerade Exponenten enthält, nennt man<br /> |
'''<colorize>ungerade Funktion</colorize>'''.<br /> | '''<colorize>ungerade Funktion</colorize>'''.<br /> | ||
|width="1%"| | |width="1%"| | ||
| − | | | + | |valign="top"|[[Datei:Punktsymmetrische Funktionen.png|380px]] |
|} | |} | ||
</popup> | </popup> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | ''Auch das lässt sich rechnerisch erklären:''<br /> | + | <big>''Auch das lässt sich rechnerisch erklären:''<br /> |
| − | Die Beziehung f (x) = - f (-x), bzw. '''f (-x) = - f (x)''' muss für alle x- Werte gelten.<br /> | + | ''Beweis:''<br /> |
| + | Die Beziehung f (x) = - f (-x), bzw. '''f (-x) = - f (x)''' muss für alle x- Werte gelten, für die die Funktion definiert ist.<br /> | ||
Setzt man negative x- Werte in die Funktionsgleichung ein, muss das den gleichen Funktionswert, aber mit verkehrtem Vorzeichen ergeben.<br /> | Setzt man negative x- Werte in die Funktionsgleichung ein, muss das den gleichen Funktionswert, aber mit verkehrtem Vorzeichen ergeben.<br /> | ||
| − | Nur wenn <span style="color: red">jeder Exponent ungerade</span> ist, dreht sich jedes Vorzeichen | + | Nur wenn <span style="color: red">jeder Exponent ungerade</span> ist, dreht sich jedes Vorzeichen vor einem x um:<br /> |
| − | Z. B.: f (x) = -x<sup | + | Z. B.: '''<span style="color: #00CD00 ">f (x) = -x<sup>5</sup> + x<sup>3</sup></span>'''<br /> |
f (-x) <br /> | f (-x) <br /> | ||
| − | = - (-x)<sup>5</sup> + (-x)<sup>3</sup><br /> | + | = - (<span style="color: red">'''-'''</span>x)<sup><span style="color: red">'''5'''</span></sup> + (<span style="color: red">'''-'''</span>x)<sup><span style="color: red">'''3'''</span></sup><br /> |
| − | = '''+'''x<sup>5</sup> '''-''' x<sup>3</sup><br /> | + | = '''<span style="color: red">+</span>'''x<sup>5</sup> '''<span style="color: red">-</span>''' x<sup>3</sup><br /> |
| − | = - ( -x<sup>5</sup> + x<sup>3</sup>)<br /> | + | = '''<span style="color: red">-</span>''' ( -x<sup>5</sup> + x<sup>3</sup>)<br /> |
| − | = '''<span style="color: red">-</span>''' f (x)<br /> | + | = '''<span style="color: red">-</span>''' f (x)<br /></big> |
<br /> | <br /> | ||
<br /> | <br /> | ||
Bereits '''ein''' gerader Exponent sorgt schon für ein falsches Vorzeichen. <br /> | Bereits '''ein''' gerader Exponent sorgt schon für ein falsches Vorzeichen. <br /> | ||
In diesem Fall läge keine Punktsymmetrie zum Ursprung vor. | In diesem Fall läge keine Punktsymmetrie zum Ursprung vor. | ||
| − | |||
| − | |||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 115: | Zeile 113: | ||
| − | <center><table border="0" width=" | + | <center><table border="0" width="850px" cellpadding=5 cellspacing=15> |
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
=== <big>Übung === | === <big>Übung === | ||
<br /> | <br /> | ||
| − | Ist die Funktion | + | Ist die Funktion achsensymmetrisch, punktsymmetrisch oder weder/noch?<br /> |
Wähle eine Rubrik aus und klicke auf alle zugehörigen Funktionen, bis das Puzzle vollständig aufgedeckt ist.<br /> | Wähle eine Rubrik aus und klicke auf alle zugehörigen Funktionen, bis das Puzzle vollständig aufgedeckt ist.<br /> | ||
<br /> | <br /> | ||
Warum wurde gerade dieses Bild als Hintergrund gewählt?</big> | Warum wurde gerade dieses Bild als Hintergrund gewählt?</big> | ||
| + | |||
<iframe src="http://LearningApps.org/watch?v=pjqfuz13j" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="http://LearningApps.org/watch?v=pjqfuz13j" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | <popup name="Bildnachweis">"Datei:Starfish.JPG" aus Wikimedia Commons (Autor: Achim Raschka)<br /> | ||
| + | http://de.wikipedia.org/wiki/Datei:Starfish.JPG#globalusage</popup> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
Aktuelle Version vom 31. August 2013, 15:58 Uhr
|
Spiegle die Punkte A, B, C, D und E im Applet am Koordinatenursprung:
|
AllgemeinWie lässt sich diese Feststellung verallgemeinern? Ist der Graph einer Funktion f punktsymmetrisch zum Ursprung,
Kannst du die Lücken der Definition auf deinem Arbeitsblatt schon ausfüllen?
|
Übung
Manipulationen an Funktionen |