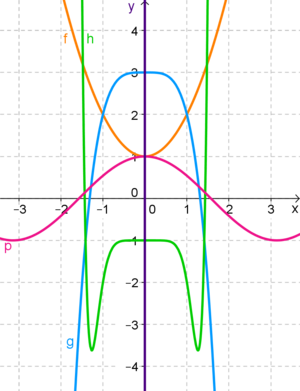
Achsensymmetrie zur y- Achse

Spiegle die Punkte A, B, C, D und E an der y- Achse. Vergleiche die Koordinaten der gespiegelten Punkte mit denen der ursprünglichen Punkte. Was fällt dir auf? Verbinde die Punkte zu einem Funktionsgraphen. Welche Funktion wird hier abgebildet? Hilfe zu GeoGebra anzeigen Hilfe zu GeoGebra verstecken Einen Punkt kannst du, wie im letzten Kapitel, über das Symbol "Neuer Punkt" in der Werkzeugleiste direkt an die jeweilige Stelle im Applet setzen. Es gibt aber auch die Möglichkeit Objekte direkt zu spiegeln: Wähle das Symbol "Spiegle Objekt an Gerade" in der Werkzeugleiste aus. Klicke zuerst den Punkt an, den du spiegeln willst, und danach die Gerade, an der der Punkt gespiegelt werden soll. In der Werkzeugleiste kannst du unter dem Symbol "Text einfügen" das Symbol "Freihandskizze erkennen" auswählen. Damit lassen sich die einzelnen Punkte zu einem Graphen verbinden. Übertrage die gespiegelten Punkte und den daraus entstandenen Funktionsgraphen auf dein Arbeitsblatt. Fülle den Lückentext aus und setze die kontrollierten Antworten auf deinem Arbeitsblatt richtig ein.

Allgemein Kannst du jetzt eine allgemeine Regel herleiten? Fülle den Lückentext aus und übertrage die kontrollierten Antworten auf dein Arbeitsblatt. MERKE: Ist der Graph einer Funktion f achsensymmetrisch zur y- Achse, so besitzen gleich weit vom Ursprung entfernte x- Werte immer den gleichen Funktionswert. Es gilt also: f (x) = f (-x). Man kann aber auch vom Funktionsterm auf den Verlauf des Graphen schließen: Gilt für eine Funktion f mit der Definitionsmenge Df für alle x ∈ Df: f (x) = f (-x), dann verläuft der Graph von f achsensymmetrisch zur y- Achse. Kennst du weitere Beispiele für achsensymmetrische Funktionen; also eine Funktion, deren Graph sich nicht verändert, wenn er an der y- Achse gespiegelt wird? Wie muss der Graph einer solchen Funktion aussehen? Worauf kommt es im Funktionsterm an? Im GeoGebra-Applet ist eine Funktion f(x) gegeben, die du noch verändern kannst. Über die Schieberegler kannst du entscheiden, ob die jeweiligen x-Potenzen im Funktionsterm auftauchen oder nicht. Stelle die Parameter a, b, c, d, e so ein, dass f achsensymmetrisch zur y- Achse ist. Kannst du bereits Teile des Definitions-Lückentextes auf deinem Arbeitsblatt ausfüllen? Wenn nicht, hilft dir diese Lösung weiter: Lösung und Definition anzeigen Lösung und Definition verstecken Beispiele wären die Funktionen f: x -> x2 + 1 g: x -> -x4 + 3 h: x -> x12 - 4x8 - 1 p: x -> cos(x) Alle ganzrationalen Funktionen haben gemeinsam, dass in ihrem Funktionsterm nur x- Potenzen mit geraden Exponenten vorkommen. Eine solche Funktion nennt man dementsprechend gerade Funktion. Woran liegt das? Beweis: Für Achsensymmetrie zur y- Achse muss immer h(x) = h(-x) für alle möglichen x- Werte einer Funktion h gelten. Gibt es nur gerade Exponenten, wird jedes negative Vorzeichen vor einem x- Wert aufgehoben: Z. B.: h: x -> x12 - 4x8 - 1 h(-x) = (-x)12 - 4 (-x)8 - 1 = (+x)12 - 4 (+x)8 - 1 = x12 - 4x8 - 1 = h(x) Sobald auch ungerade Exponenten im Funktionsterm vorkommen, sind deren Vorzeichen falsch und die Funktion ist nicht mehr achsensymmetrisch zur y- Achse: Z. B.: k(x) = x12 - 4x9 - 1 k(-x) = (-x)12 - 4(-x)9 - 1 = (+x)12 - 4 (-x)9 - 1 = x12 + 4x9 - 1 ≠ k(x)

Übung Ist die Funktion gerade oder nicht? Ordne die Funktionsterme und Graphen der richtigen Seite zu. Zurück zur Symmetrie von Funktionsgraphen Weiter zur Punktsymmetrie zum Ursprung Manipulationen an Funktionen