Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Punktsymmetrie zum Ursprung: Unterschied zwischen den Versionen
K |
|||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 38: | Zeile 38: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | === <big>Allgemein</big> | + | === <big>Allgemein === |
| + | |||
| + | Wie lässt sich diese Feststellung verallgemeinern?<br /> | ||
| + | Setze die richtigen Lücken ein und übertrage sie anschließend auf dein Arbeitsblatt.<br /></big> | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 62: | Zeile 65: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | <popup name="Lösung"> | + | |
| + | <big>Kannst du die Lücken der Definition auf deinem Arbeitsblatt schon ausfüllen?<br /> | ||
| + | Kontrolliere dich mit der folgenden Lösung:<br /></big> | ||
| + | <br /> | ||
| + | <popup name="Lösung und Definition"> | ||
{| | {| | ||
| valign="top"| | | valign="top"| | ||
| Zeile 72: | Zeile 79: | ||
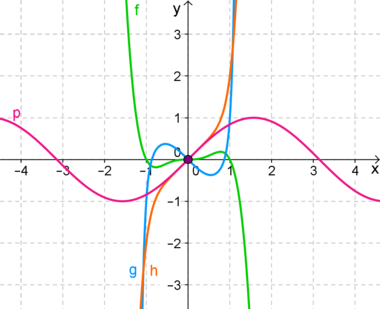
| − | Bei den ganzrationalen Funktionen dürfen <span style="color: red">nur | + | Bei den ganzrationalen Funktionen dürfen <span style="color: red">nur x- Potenzen mit <u>ungeraden</u> Exponenten</span> im Funktionsterm auftauchen, also x<sup>1</sup>, x<sup>3</sup>, x<sup>5</sup>, ...<br /> |
<br /> | <br /> | ||
| − | Eine Funktion, die nur ungerade Exponenten enthält, nennt man<br /> | + | Eine ganzrationale Funktion, die nur ungerade Exponenten enthält, nennt man<br /> |
'''<colorize>ungerade Funktion</colorize>'''.<br /> | '''<colorize>ungerade Funktion</colorize>'''.<br /> | ||
|width="1%"| | |width="1%"| | ||
| − | |valign="top"|[[Datei:Punktsymmetrische Funktionen.png| | + | |valign="top"|[[Datei:Punktsymmetrische Funktionen.png|380px]] |
|} | |} | ||
</popup> | </popup> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | ''Auch das lässt sich rechnerisch erklären:''<br /> | + | <big>''Auch das lässt sich rechnerisch erklären:''<br /> |
| + | ''Beweis:''<br /> | ||
Die Beziehung f (x) = - f (-x), bzw. '''f (-x) = - f (x)''' muss für alle x- Werte gelten, für die die Funktion definiert ist.<br /> | Die Beziehung f (x) = - f (-x), bzw. '''f (-x) = - f (x)''' muss für alle x- Werte gelten, für die die Funktion definiert ist.<br /> | ||
Setzt man negative x- Werte in die Funktionsgleichung ein, muss das den gleichen Funktionswert, aber mit verkehrtem Vorzeichen ergeben.<br /> | Setzt man negative x- Werte in die Funktionsgleichung ein, muss das den gleichen Funktionswert, aber mit verkehrtem Vorzeichen ergeben.<br /> | ||
| − | Nur wenn <span style="color: red">jeder Exponent ungerade</span> ist, dreht sich jedes Vorzeichen | + | Nur wenn <span style="color: red">jeder Exponent ungerade</span> ist, dreht sich jedes Vorzeichen vor einem x um:<br /> |
| − | Z. B.: f (x) = -x<sup | + | Z. B.: '''<span style="color: #00CD00 ">f (x) = -x<sup>5</sup> + x<sup>3</sup></span>'''<br /> |
f (-x) <br /> | f (-x) <br /> | ||
| − | = - (-x)<sup>5</sup> + (-x)<sup>3</sup><br /> | + | = - (<span style="color: red">'''-'''</span>x)<sup><span style="color: red">'''5'''</span></sup> + (<span style="color: red">'''-'''</span>x)<sup><span style="color: red">'''3'''</span></sup><br /> |
| − | = '''+'''x<sup>5</sup> '''-''' x<sup>3</sup><br /> | + | = '''<span style="color: red">+</span>'''x<sup>5</sup> '''<span style="color: red">-</span>''' x<sup>3</sup><br /> |
| − | = - ( -x<sup>5</sup> + x<sup>3</sup>)<br /> | + | = '''<span style="color: red">-</span>''' ( -x<sup>5</sup> + x<sup>3</sup>)<br /> |
| − | = '''<span style="color: red">-</span>''' f (x)<br /> | + | = '''<span style="color: red">-</span>''' f (x)<br /></big> |
<br /> | <br /> | ||
<br /> | <br /> | ||
Bereits '''ein''' gerader Exponent sorgt schon für ein falsches Vorzeichen. <br /> | Bereits '''ein''' gerader Exponent sorgt schon für ein falsches Vorzeichen. <br /> | ||
In diesem Fall läge keine Punktsymmetrie zum Ursprung vor. | In diesem Fall läge keine Punktsymmetrie zum Ursprung vor. | ||
| − | |||
| − | |||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 112: | Zeile 118: | ||
=== <big>Übung === | === <big>Übung === | ||
<br /> | <br /> | ||
| − | Ist die Funktion | + | Ist die Funktion achsensymmetrisch, punktsymmetrisch oder weder/noch?<br /> |
Wähle eine Rubrik aus und klicke auf alle zugehörigen Funktionen, bis das Puzzle vollständig aufgedeckt ist.<br /> | Wähle eine Rubrik aus und klicke auf alle zugehörigen Funktionen, bis das Puzzle vollständig aufgedeckt ist.<br /> | ||
<br /> | <br /> | ||
Warum wurde gerade dieses Bild als Hintergrund gewählt?</big> | Warum wurde gerade dieses Bild als Hintergrund gewählt?</big> | ||
| + | |||
<iframe src="http://LearningApps.org/watch?v=pjqfuz13j" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="http://LearningApps.org/watch?v=pjqfuz13j" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | <popup name="Bildnachweis">"Datei:Starfish.JPG" aus Wikimedia Commons (Autor: Achim Raschka)<br /> | ||
| + | http://de.wikipedia.org/wiki/Datei:Starfish.JPG#globalusage</popup> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
Aktuelle Version vom 31. August 2013, 15:58 Uhr
|
Spiegle die Punkte A, B, C, D und E im Applet am Koordinatenursprung:
|
AllgemeinWie lässt sich diese Feststellung verallgemeinern? Ist der Graph einer Funktion f punktsymmetrisch zum Ursprung,
Kannst du die Lücken der Definition auf deinem Arbeitsblatt schon ausfüllen?
|
Übung
Manipulationen an Funktionen |