Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).KW 12: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 48: | Zeile 48: | ||
<br /> | <br /> | ||
====Lösungen der Aufgaben aus KW 12:<br />==== | ====Lösungen der Aufgaben aus KW 12:<br />==== | ||
| + | {| | ||
| + | |- | ||
| + | | [[Datei:KW12 Aufgabe1.JPG|thumb|Lösungen der Aufgaben aus KW 12 Aufgabe 1]] || [https://ggbm.at/zg72w6Hr Aufgabe 1 - zeichnerisch] || [[Datei:KW12 Aufgabe2.JPG|thumb|Lösungen der Aufgaben aus KW 12 Aufgabe 2]] || [[Datei:KW12 Aufgabe3.JPG|thumb|Lösungen der Aufgaben aus KW 12 Aufgabe 3]] | ||
| + | |} | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Zeile 53: | Zeile 57: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | <iframe src="https://learningapps.org/watch?v= | + | <iframe src="https://learningapps.org/watch?v=pfk90i4wc18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
Aktuelle Version vom 18. April 2018, 21:45 Uhr
Inhaltsverzeichnis |
Wochenplan KW 12
Besprechung Mi 11.04.
- grüne Aufgaben sind Pflichtaufgaben
- orange Aufgaben sind optional zur vertiefenden Übung
Aufgabe I
Bestimme die Schnittpunkte der Graphen folgender Funktionen zeichnerisch und rechnerisch.
| a) | 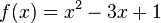
|
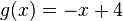
|
| b) | 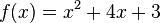
|
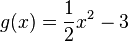
|
| c) | 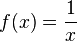
|
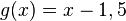
|
Aufgabe II
Bestimme die Definitions- und die Lösungsmenge folgender Gleichungen.
- a)
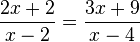
- b)
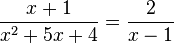
Aufgabe III
Ein Parallele 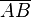 zur y-Achse schneidet den Graphen von
zur y-Achse schneidet den Graphen von 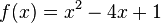 in
in 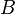 und den von
und den von 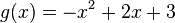 in
in 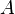 .
.
- a) Für welche Lage von
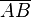 wird die Länge der Strecke am kleinsten?
wird die Länge der Strecke am kleinsten?
- b) Für welche Lage von
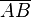 wird die Länge der Strecke am größten, wenn sich
wird die Länge der Strecke am größten, wenn sich 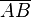 nur innerhalb der beiden Schnittpunkte der Funktionsgraphen befindet.
nur innerhalb der beiden Schnittpunkte der Funktionsgraphen befindet.
- Kontrolliere deine Ergebnisse, indem du den Punkt
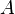 auf dem Graphen verschiebst.
auf dem Graphen verschiebst.
Lösungen der Aufgaben aus KW 12:
| Aufgabe 1 - zeichnerisch |




