Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).KW 38: Unterschied zwischen den Versionen
| Zeile 56: | Zeile 56: | ||
====<span style="color:green">Aufgabe III</span>==== | ====<span style="color:green">Aufgabe III</span>==== | ||
Bearbeite die fehlenden Aufgaben auf deinem Übungsblatt. | Bearbeite die fehlenden Aufgaben auf deinem Übungsblatt. | ||
| + | <br /> | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | [[Datei:Uebungsblatt Wurzeln.pdf|left|thumb|Übungsblatt Wurzeln]] | ||
| + | |} | ||
| + | <br /> | ||
| + | |||
| + | ---- | ||
| + | ==== Verbesserung ==== | ||
Version vom 13. Oktober 2018, 18:13 Uhr
Inhaltsverzeichnis |
Wochenplan KW 38
Besprechung Di 25.09.
- grüne Aufgaben sind Pflichtaufgaben
- orange Aufgaben sind optional zur vertiefenden Übung
Aufgabe I
Zur Erläuterung des Beweisverfahrens, dass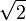 
irrational ist, hier ein Beispiel außerhalb der Mathematik, das die Idee des Widerspruchsbeweises darstellen soll.
Wir behaupten: "Ein Monat hat höchstens fünf Sonntage."
Annahme: Ein Monat hat mindestens sechs Sonntage.
Zwischen den sechs Sonntagen würden fünf Wochen verstreichen. Also hätte der Montag mindestens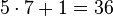 
Tage.
Das ist ein Widerspruch zur Voraussetzung, dass ein Monat höchstens 31 Tage hat. Somit muss die Annahme falsch sein.
Beweise nun, dass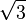 
irrational ist.
Aufgabe II
Begründe welche Aussagen richtig sind und welche falsch.
| a) |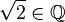 
|
b) |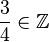 
|
| c) |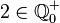 
|
d) |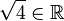 
|
| e) |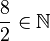 
|
f) |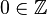 
|
| g) |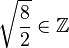 
|
h) |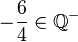 
|
| i) |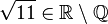 
|
j) |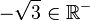 
|
Aufgabe III
Bearbeite die fehlenden Aufgaben auf deinem Übungsblatt.
  |
