Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Gemischte Aufgaben: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 47: | Zeile 47: | ||
<math>f(x)=(x+2)x(x-3)^2</math> | <math>f(x)=(x+2)x(x-3)^2</math> | ||
| + | </popup> | ||
| + | }} | ||
| + | |||
| + | {{Aufgaben|3| <iframe src="https://learningapps.org/watch?v=pj2vfft2n19" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | <popup Name="Lösung"> | ||
| + | '''Wahr''' | ||
| + | |||
| + | Es gibt keine ganzrationale Funktion dritten Grades ohne Nullstellen. Begründung: Da eine ganzrationale Funktion dritten Grades ein unterschiedliches Unendlichkeitsverhalten für x->∞ und x->-∞ aufweist, hat der Graph zwangsläufig eine Nullstelle. | ||
| + | |||
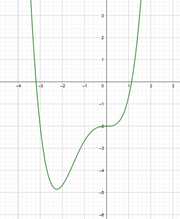
| + | Gegeben sei die Funktion $$f(x)=x^3-2x^2+1$$. Durch Verschieben des Graphen kann man die Anzahl der Nullstellen verändern. Begründung: Durch eine Verschiebung entlang der y-Achse kann man die Anzahl der Nullstellen verändern. Verschiebung anhand der x-Achse klappt allerdings nicht. | ||
| + | |||
| + | '''Falsch''' | ||
| + | |||
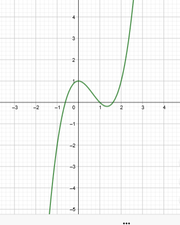
| + | Der Graph einer ungeraden Funktion verläuft durch den Ursprung. Begründung: Gegenbeispiel: <math>f(x)=x^3-1</math> | ||
| + | |||
| + | Eine ganzrationale Funktion dritten Gerades hat genau drei Nullstellen. Begründung: Sie hat maximal drei Nullstellen, kann aber auch weniger haben (<math>f(x)=x^3</math> hat nur eine Nullstelle bei x=0). | ||
| + | |||
| + | Wenn eine ganzrationale gerade Funktion eine Nullstelle hat, dann hat sie eine weitere Nullstelle. Begründung: Gegenbeispiel: <math>f(x)=x^4</math> hat nur bei 0 eine Nullstelle. | ||
| + | |||
| + | Durch Stauchen des Graphen einer ganzrationalen Funktion kann man das Verhalten des Graphen für x gegen Unendlich verändern. Begründung: Egal wie sehr die Funktion gestaucht wird, früher oder später bleibt das Unendlichkeitsverhalten gleich. | ||
</popup> | </popup> | ||
}} | }} | ||
Version vom 21. November 2019, 16:34 Uhr
 Aufgabe 1 Graphen skizzieren
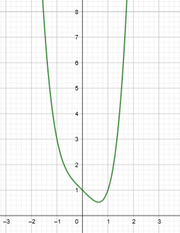
Skizziere folgende Graphen. Achte dabei auf das Verhalten nahe Null und gegen Unendlich sowie auf die Symmetrie. a)
b)
c)
|
Aufgabe 2 Funktionsgleichung aufstellen
Bestimme mit den gegebenen Eigenschaften eine passende Funktionsgleichung einer ganzrationalen Funktion. a) Die Graph ist punksymmetrisch zum Ursprung und besitzt genau 3 Nullstellen. b) Die Graph ist achsensymmetrisch zur y-Achse, hat mindestens Grad 3 und besitzt keine Nullstellen. c)
Der Graph geht für x->-∞ und für x->∞ gegen ∞ und verhält sich nahe Null wie d) Der Graph hat einfache Nullstellen bei -2 und 0 sowie eine doppelte bei 3. |
.
| Aufgabe 3
|
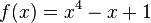
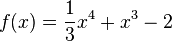
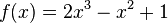
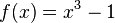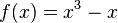
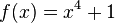
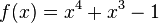
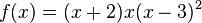
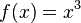hat nur eine Nullstelle bei x=0).
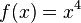hat nur bei 0 eine Nullstelle.
