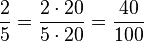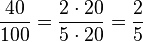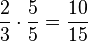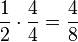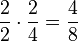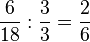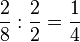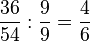Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Erweitern und Kürzen: Unterschied zwischen den Versionen
K |
|||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<u></u><div style="padding:50px;background:#0000FF;border:0px groove;"> | <u></u><div style="padding:50px;background:#0000FF;border:0px groove;"> | ||
| − | + | <div style="margin:0; margin-right:50px; margin-left:50px; border:5px solid #FFFFFF; padding: 1em 1em 1em 1em; background-color:#FFFFFF; align:left;"> | |
| − | <div style="margin:0; margin-right: | + | |
<big><span style="color:#C00000"> | <big><span style="color:#C00000"> | ||
| + | [[Datei:Gemeiner Bruch.svg|miniatur]] | ||
| + | <span style="color: #4CC417"><u>'''Was ist überhaupt ein Bruch?'''</u></span> | ||
| − | < | + | Ganz einfach: Ein Bruch ist ein Teil eines Ganzen!<br /> |
| − | + | So repräsentiert z.B. der Bruch <math>\frac{3}{4}</math> 3 Teile eines Ganzen, das aus insgesamt 4 Teilen besteht. | |
| + | Als '''Bruchrechnung''' bezeichnet man das Rechnen mit ''gemeinen Brüchen'' in der „Zähler-Bruchstrich-Nenner-Schreibweise“. | ||
| + | Wenn du mit Brüchen rechnen willst, musst du in der Lage sein, sie richtig zu kürzen oder zu erweitern. Das brauchst du immer wieder für die verschiedenen Bruchrechnungen. Also pass gut auf!<br /> | ||
| − | |||
| − | + | -> <span style="color: turquoise"><u>'''Erweitern und Kürzen:'''</u> | |
| + | <u></u></span> | ||
| − | + | <span style="color: turquoise"><u>Erweitern:</u></span> Multipliziere Zähler und Nenner des Bruches mit derselben natürlichen Zahl, welche nicht 0 sein darf! | |
| − | + | Bsp.: Erweitere den Bruch <math>\frac{2}{5}</math> mit 20.<br /> | |
| + | <math> \frac{2}{5}= \frac{2\cdot20}{5\cdot20} = \frac{40}{100} </math> | ||
| + | <br /> | ||
| − | + | <span style="color: turquoise"><u>Kürzen:</u></span> Dividiere Zähler und Nenner des Bruches durch dieselbe natürliche Zahl, welche nicht 0 sein darf! | |
| − | + | Bsp.: Kürze den Bruch <math>\frac{40}{100}</math> soweit es geht.<br /> | |
| − | < | + | |
| − | < | + | <math> \frac{40}{100}= \frac{2\cdot20}{5\cdot20} = \frac{2}{5} </math> |
| − | |||
| + | <div class="lueckentext-quiz"> | ||
| − | + | Beim '''Erweitern''' bzw. Kürzen muss man Zähler und '''Nenner''' mit der gleichen Zahl multiplizieren bzw. dividieren. | |
| + | </div> | ||
| + | |||
| + | |||
| + | Nun gibt es hier ein kleines Beispiel, mit dem du testen kannst, ob du die Grundregeln verstanden hast. '''Viel Spaß!'''<br /> | ||
| − | |||
=== Zuordnungs-Quiz === | === Zuordnungs-Quiz === | ||
| Zeile 41: | Zeile 48: | ||
<div class="zuordnungs-quiz" > | <div class="zuordnungs-quiz" > | ||
{| | {| | ||
| − | | Erweitern || <math> \frac{2}{3} | + | | Erweitern || <math> \frac{2}{3}\cdot\frac{5}{5}=\frac{10}{15}</math> || <math> \frac{1}{2}\cdot\frac{4}{4}=\frac{4}{8}</math>|| <math> \frac{2}{2}\cdot\frac{2}{4}=\frac{4}{8}</math> |
|- | |- | ||
| Zeile 48: | Zeile 55: | ||
|| <math> \frac{36}{54}:\frac{9}{9}=\frac{4}{6}</math> | || <math> \frac{36}{54}:\frac{9}{9}=\frac{4}{6}</math> | ||
|} | |} | ||
| + | |||
</div> | </div> | ||
|} | |} | ||
| + | |||
| + | |||
| + | Hier gibt es nun weitere Aufgaben für dich zum Üben: | ||
| + | |||
| + | <u>Aufgabe 1</u> | ||
| + | <popup name= Aufgabe> | ||
| + | <iframe src="https://learningapps.org/watch?app=117450" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | </popup> | ||
| + | |||
| + | |||
| + | <u>Aufgabe 2</u> | ||
| + | <popup name= Aufgabe> | ||
| + | <iframe src="https://learningapps.org/watch?app=4525567" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | </popup> | ||
| + | |||
| + | |||
| + | <u>Aufgabe 3</u> | ||
| + | <popup name= Aufgabe> | ||
| + | <iframe src="https://learningapps.org/watch?app=1574480" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | </popup> | ||
| + | |||
Aktuelle Version vom 9. Januar 2020, 11:58 Uhr
Was ist überhaupt ein Bruch?
Ganz einfach: Ein Bruch ist ein Teil eines Ganzen!
So repräsentiert z.B. der Bruch 
3 Teile eines Ganzen, das aus insgesamt 4 Teilen besteht.
Als Bruchrechnung bezeichnet man das Rechnen mit gemeinen Brüchen in der „Zähler-Bruchstrich-Nenner-Schreibweise“.
Wenn du mit Brüchen rechnen willst, musst du in der Lage sein, sie richtig zu kürzen oder zu erweitern. Das brauchst du immer wieder für die verschiedenen Bruchrechnungen. Also pass gut auf!
-> Erweitern und Kürzen:
Erweitern: Multipliziere Zähler und Nenner des Bruches mit derselben natürlichen Zahl, welche nicht 0 sein darf!
Bsp.: Erweitere den Bruch 
mit 20.
Kürzen: Dividiere Zähler und Nenner des Bruches durch dieselbe natürliche Zahl, welche nicht 0 sein darf!
Bsp.: Kürze den Bruch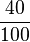 
soweit es geht.
Beim Erweitern bzw. Kürzen muss man Zähler und Nenner mit der gleichen Zahl multiplizieren bzw. dividieren.
Nun gibt es hier ein kleines Beispiel, mit dem du testen kannst, ob du die Grundregeln verstanden hast. Viel Spaß!
Zuordnungs-Quiz
|
Hier gibt es nun weitere Aufgaben für dich zum Üben:
Aufgabe 1
Aufgabe 2
Aufgabe 3
| zur Berechnung von Grundwert, Prozentsatz und Prozentwert | zu Brüche als Quotienten |
