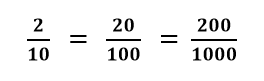Achtung:

Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.

Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.

Gerne kannst Du natürlich weiterarbeiten

im neuen Projektwiki (projekte.zum.de).

Dezimalbrüche: Unterschied zwischen den Versionen

Aus Projektwiki - ein Wiki mit Schülern für Schüler.
Wechseln zu: Navigation, Suche
 
(15 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 2: Zeile 2:
  
  
−
<div style="margin:0; margin-right:250px; margin-left:250px; border:5px solid #FFFFFF; padding: 1em 1em 1em 1em; background-color:#FFFFFF; align:left;">
+
<div style="margin:0; margin-right:50px; margin-left:50px; border:5px solid #FFFFFF; padding: 1em 1em 1em 1em; background-color:#FFFFFF; align:left;">
 
<big><span style="color:#C00000">&nbsp;
 
<big><span style="color:#C00000">&nbsp;
  
−
In dem Nenner eines Dezimalbruchs steht eine natürliche Zahl der Zehnerpotenz.  
+
Im <span style="color:#436EEE "><u>'''Nenner'''</u></span> eines Dezimalbruchs steht immer eine natürliche Zahl der <span style="color:#436EEE "><u>'''Zehnerpotenz'''</u></span>.  
  
−
Mit anderen Worten: Ein Bruch in dessen Nenner 10, 100, 1000, usw… steht. Deshalb wird der Dezimalbruch auch häufig als Zehnerbruch bezeichnet!
+
Mit anderen Worten: Ein Bruch in dessen Nenner 10, 100, 1000, usw… steht, ist ein Dezimalbruch. Deshalb wird der Dezimalbruch auch häufig als <span style="color:#436EEE "><u>'''Zehnerbruch'''</u></span> bezeichnet!
  
 
Hier ein Beispiel eines Dezimalbruchs:
 
Hier ein Beispiel eines Dezimalbruchs:
  
−
[[Datei:Bruch 2 10.PNG|300px|links|]]
+
[[Datei:Bruch 2 10.PNG|300px|gerahmt|links|]]
−
 
+
<br/>
 
<br/>
 
<br/>
 
<br/>
 
<br/>
Zeile 20: Zeile 20:
 
In Dezimalschreibweise:  '''0,2 = 0,20 = 0,200'''
 
In Dezimalschreibweise:  '''0,2 = 0,20 = 0,200'''
  
−
Wie zu erkennen ist kann man bei diesem Beispiel Arbeit ersparen und die '''Nullen am Ende weglassen''', da sich die vorliegende Zahl dadurch '''nicht verändert'''.
+
Wie zu erkennen ist, kann man sich bei diesem Beispiel Arbeit ersparen und die <span style="color:#436EEE "><u>'''Nullen am Ende weglassen'''</u></span>, da sich die Zahl dadurch <span style="color:#436EEE "><u>'''nicht verändert'''</u></span>.
  
−
Natürlich kommen nicht nur Zehnerbrüche in der Mathematik vor. Deshalb sollest du wissen wie man einen '''Bruch in einen Dezimalbruch''' umwandelt.  
+
Natürlich kommen nicht nur Zehnerbrüche in der Mathematik vor. Deshalb solltest du wissen, wie man einen  
 +
<span style="color:#436EEE "><u>'''Bruch in einen Dezimalbruch'''</u></span> umwandelt.  
  
−
Prüfe dazu, '''ob''' du den vorliegenden Bruch auf eine '''Zehnerpotenz erweitern''' oder '''kürzen''' kannst.
+
Prüfe dazu, ob du den vorliegenden Nenner auf eine <span style="color:#436EEE "><u>'''Zehnerpotenz erweitern'''</u></span> oder <span style="color:#436EEE "><u>'''kürzen'''</u></span> kannst.
  
 
Hier ein paar Beispiele:
 
Hier ein paar Beispiele:
Zeile 36: Zeile 37:
 
  <math>\frac{12}{16}</math> = <math>\frac{3}{4}</math> = <math>\frac{75}{100}</math> = '''0,75'''
 
  <math>\frac{12}{16}</math> = <math>\frac{3}{4}</math> = <math>\frac{75}{100}</math> = '''0,75'''
  
−
Der Bruch  '''<math>\frac{1}{3}</math>'''  kann beispielsweise '''nicht''' auf eine '''Zehnerpotenz''' erweitert werden und kann daher nur gerundet angegeben werden:
+
Der Bruch  '''<math>\frac{1}{3}</math>'''  kann beispielsweise <span style="color:#436EEE "><u>'''nicht'''</u></span> auf eine <span style="color:#436EEE "><u>'''Zehnerpotenz'''</u></span> erweitert werden, weil keine Zehnerpotenz durch 3 teilbar ist. Daher kann der Bruch <math>\frac{1}{3}</math> nur gerundet angegeben werden:  
  
 
  <math>\frac{1}{3}</math> = <math>\frac{3}{9}</math> '''&#x2248; 0,33'''
 
  <math>\frac{1}{3}</math> = <math>\frac{3}{9}</math> '''&#x2248; 0,33'''
  
  
−
Diese Dezimalbrüche solltest du dir sorgfältig einprägen, da sie häufig in Aufgaben verwendet werden!
+
Diese Dezimalbrüche solltest du dir <span style="color:#436EEE "><u>'''sorgfältig einprägen'''</u></span>, da sie <span style="color:#436EEE "><u>'''häufig'''</u></span> in Aufgaben verwendet werden!
  
 
  <math>\frac{1}{2}</math> '''= 0,5
 
  <math>\frac{1}{2}</math> '''= 0,5
Zeile 59: Zeile 60:
 
Übe nun den Umgang mit Dezimalbrüchen in den folgenden Aufgaben. Viel Spaß!
 
Übe nun den Umgang mit Dezimalbrüchen in den folgenden Aufgaben. Viel Spaß!
  
−
<iframe src="https://learningapps.org/watch?v=pf7mmsaq318" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
+
<div style="padding:10px;background:#8B1A1A;border:0px groove;">
  
−
<iframe src="https://learningapps.org/watch?v=pbfip3r7n18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
+
<popup name= 1.Aufgabe>
  
 +
<iframe src="https://learningapps.org/watch?v=pf7mmsaq318" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
  
 +
</popup>
  
−
Hier geht's zum nächsten Kapitel!
+
<br/>
 +
 
 +
<popup name= 2.Aufgabe>
 +
 
 +
<iframe src="https://learningapps.org/watch?v=pbfip3r7n18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
 +
 
 +
</popup>
 +
 
 +
<br/>
 +
 
 +
<popup name= 3.Aufgabe>
 +
 
 +
<iframe src="https://learningapps.org/watch?v=p1drtue5j18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
 +
 
 +
</popup>
 +
 
 +
</div>
 +
 
 +
<br/>
 +
<br/>
  
 
{{Vorlage:Lesepfad Ende
 
{{Vorlage:Lesepfad Ende
−
|Link zurück=[[Julius-Echter-Gymnasium/Mathematik/Brüche_als_Quotienten|zu Brüche als Quotienten]]                   
+
|Link zurück=[[Julius-Echter-Gymnasium/Mathematik/Brüche_als_Quotienten|zu Brüchen als Quotienten]]                   
 
|Link vor=[[Julius-Echter-Gymnasium/Mathematik/Runden_von_Dezimalzahlen|zum Runden von Dezimalzahlen]]
 
|Link vor=[[Julius-Echter-Gymnasium/Mathematik/Runden_von_Dezimalzahlen|zum Runden von Dezimalzahlen]]
 
|Text Copyright=
 
|Text Copyright=
 
}}
 
}}

Aktuelle Version vom 9. Januar 2020, 12:21 Uhr


 

Im Nenner eines Dezimalbruchs steht immer eine natürliche Zahl der Zehnerpotenz.

Mit anderen Worten: Ein Bruch in dessen Nenner 10, 100, 1000, usw… steht, ist ein Dezimalbruch. Deshalb wird der Dezimalbruch auch häufig als Zehnerbruch bezeichnet!

Hier ein Beispiel eines Dezimalbruchs:

Bruch 2 10.PNG







In Dezimalschreibweise: 0,2 = 0,20 = 0,200

Wie zu erkennen ist, kann man sich bei diesem Beispiel Arbeit ersparen und die Nullen am Ende weglassen, da sich die Zahl dadurch nicht verändert.

Natürlich kommen nicht nur Zehnerbrüche in der Mathematik vor. Deshalb solltest du wissen, wie man einen Bruch in einen Dezimalbruch umwandelt.

Prüfe dazu, ob du den vorliegenden Nenner auf eine Zehnerpotenz erweitern oder kürzen kannst.

Hier ein paar Beispiele: 

\frac{1}{5} = \frac{2}{10} = 0,2


\frac{1}{4} = \frac{25}{100} = 0,25


\frac{12}{16} = \frac{3}{4} = \frac{75}{100} = 0,75

Der Bruch \frac{1}{3} kann beispielsweise nicht auf eine Zehnerpotenz erweitert werden, weil keine Zehnerpotenz durch 3 teilbar ist. Daher kann der Bruch \frac{1}{3} nur gerundet angegeben werden: 

\frac{1}{3} = \frac{3}{9} ≈ 0,33


Diese Dezimalbrüche solltest du dir sorgfältig einprägen, da sie häufig in Aufgaben verwendet werden! 

\frac{1}{2} = 0,5


\frac{1}{4} = 0,25


\frac{1}{8} = 0,125


\frac{1}{10} = 0,1


\frac{1}{16} = 0,0625

Übe nun den Umgang mit Dezimalbrüchen in den folgenden Aufgaben. Viel Spaß!



zu Brüchen als Quotienten zum Runden von Dezimalzahlen

Von „https://projektwiki.zum.de/index.php?title=Julius-Echter-Gymnasium/Mathematik/Dezimalbrüche&oldid=80203“