|
|
| (39 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| | __NOTOC__ | | __NOTOC__ |
| − | === Wiederholung: Verschiebung von Parabeln === | + | <div style="padding:1px;background:#1C86EE;border:0px groove;"> |
| − | Du weißt bereits, wie sich Parameter auf die Graphen von Parabeln auswirken können.
| + | |
| | | | |
| − | Im folgenden Applet kannst du über die Funktionen h bzw. g die Verschiebung nach links/rechts (durch den Schieberegler a) bzw. nach oben/unten (durch den Schieberegler b) beobachten.<br>
| |
| − | Klicke auf die jeweiligen Checkboxen im Applet, um die Funktionen anzuzeigen oder auszublenden.
| |
| − |
| |
| − | In der Funktion j werden beide Arten der Verschiebung zusammengeführt.
| |
| − |
| |
| − | <ggb_applet width="1016" height="666" version="3.2" ggbBase64="UEsDBBQACAAIAEdXsUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVjRcps4FH3efoVGDzvJ7MQBjB171qSz233pTLrZmbR96MPuCLgGJYBYIRLcz+on9Mv2SgKDHdd1Nk7tB+DqIu495+gge/G6yTNyD7LiogioO3IogSISMS+SgNZqeTajry9fLRIQCYSSkaWQOVMBHY88quM1v3z106JKxQNhmUn5yOEhoEuWVUBJVUpgcZUCqI04qxuecSZX1+EtRKrqB+wkb4uyVutglMdXvMJrJWug5+aJZcbVH/yexyBJJqKATidYO559BKl4xLKA+o6NeAH1tgYxNNajqZD8syiUTu8nz1gIGSJwo1YZEHKvR8d2aInJhFT8MyBavo4tzg0IC6ijjMecFbpRUyImEfLAY5ViruNO8XHAkxT7mE4ndrpICBnfrCoFOWk+gRRYtTsbOd58NvcmU3c+G/uUrOzI2B+PLuaeM7df1xkjwNgMljJ1Rv588Jnhw1b92MQZfNpO4P4GlMIuK8IaqNr+SSJ5vAZeX7ytfhdZHyoFL9QbVqpaGo2M25DBKqCIqdQ9/lYkGbQxDxlMIboLRXNjgRvbqd+vSnOLqSdM3ohMSCI1WxNMaI+hPZocXeg6yzE5jslo59CTrsfduWcyzDG0R0svL2xpbeNu17XrdI/hFdEBnFxLu8PG6CKglNQFV1fdBQrqru3Utfl/1nmIS2ooqfWU7pGmXJxvCW5xB7KAzKqqQGJrUVdWu5Y6U0cMEc/x0g60gDBN1gcswEZjSCR0ddv1aOEyo85QuVvhxXlXhK6hwlojhcaC/SjdC66+Kko5hHWRkHuM/8WkbrnQhqBwLQb03UpylpMrLImSmCm8S/sMNGgklTYpixjBptCpmhKPJ80pCUjz94k3ck5NFZBBDrhOldHXsi5MFWuwl3RTBSpFuAucPqCoNzUUpTE2YTxqi7GeWhz+hibRzcqU4dnI6YxlhXY1hNHMdr1cVqBIY+5Zac77sXcihg0HYgUSaFBF1yj15FoiJUDc+nfXACnxcWaNDvg/oGtUlsXvEZJFnYPk0RoDZoDE4upOBKP/iVu34i1yE3cAnbsXuh6eNq/KzCsh5/g6O/M1HjlDYM0ZCyuR1QpuItR3cSUig2NX4NqpdReajJnvjSwhno0teQO9E37j3bELYG9LVs/h8HB6wqPRY2WtadFu7PgH09Mre7ZH2S9J3djz91P3vcXxYtxtWVpA30Oj3NbVfv63FurXztu+frHXO9xN4U10c4b9DA/6fb5z9Ry2UYOzjQxefjvJI4aoi4mhaeru13YoRAas9/DoH3db3YPGjqjvQ517Nmm925ntw6fbCHWC7OuJcE+lUTHZyZp48gsJnwZNfERg9vjy4cC4BpiLyRFwSS0uJw05I+z065enIQPHREarZI3MMzXj7/bFp2Fzu4XNTuU8Mp20NZxNZNvNFDlgN5UedzeF+8aYW3vF7Os2OX4RaZ65F/b1vnfD9dQt0yOIkxbiZGOnaug5BODkRwCs/fQlbPHM876/pX02wrctwrc7RHwwzrc/AucXchK/3aYeEeXz4S848zdH+x/Q5X9QSwcIx0W/rIUEAAA1EgAAUEsBAhQAFAAIAAgAR1exQsdFv6yFBAAANRIAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAC/BAAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
| |
| − |
| |
| − | <br>
| |
| − | <br>
| |
| − | Auch andere Funktionsgraphen lassen sich derartig verschieben. <br>
| |
| − | Im folgenden wollen wir untersuchen, welchen Einfluss Parameter in einer Funktionsgleichung auf den Verlauf des Graphens der Funktion haben.
| |
| − | <br>
| |
| − | Fülle parallel zum Lernpfad das Arbeitsblatt aus, auf dem alle wichtigen Informationen zusammengefasst werden:
| |
| − | <br>
| |
| − | [[Datei:AB Verschieben.pdf]]
| |
| − | <br>
| |
| − |
| |
| − | === Verschiebung nach links/rechts ===
| |
| − |
| |
| − |
| |
| − | Fülle den ersten Abschnitt auf deinem Arbeitsblatt aus:<br />
| |
| − | <br>
| |
| | | | |
| | + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> |
| | + | <tr><td width="800px" valign="top"> |
| | {| | | {| |
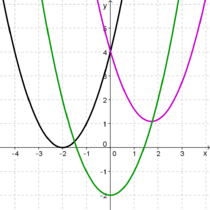
| − | | + | | valign="top"|In der 9. Klasse lernst du, welchen Einfluss die Parameter '''<span style="color: #FF7F00 ">a</span>''', '''<span style="color:#FF7F00 ">b</span>''' oder '''<span style="color:#FF7F00 ">c</span>''' auf eine Parabel, also auf den Graphen einer quadratischen Funktion mit dem Funktionsterm<br /> |
| − | |width="40%"|[[Datei:Verschiebung nach rechts.png|400px]] | + | f (x) = '''<span style="color:#FF7F00 ">a</span>'''x<sup>2</sup> + '''<span style="color: #FF7F00 ">b</span>'''x + '''<span style="color: #FF7F00 ">c</span>''',<br /> |
| − | | + | haben.<br /> |
| − | |width="3%"|
| + | |
| − | | + | |
| − | |valign="top"|Vergleiche die beiden Graphen an den vorgegebenen Werten:<br>
| + | |
| − | | + | |
| − | *h('''1,5''') = -3,375 = f (-1,5) = f ('''1,5''' - ____)
| + | |
| | <br /> | | <br /> |
| − | *h(3) = _____ = f (___) = f (_____ - _____)
| + | Oft wird auch die Scheitelform einer quadratischen Funktion<br /> |
| | + | f (x) = (x - '''<span style="color:#FF7F00 ">d</span>''')<sup>2</sup> + '''<span style="color: #FF7F00 ">e</span>'''<br /> |
| | + | betrachtet.<br /> |
| | + | In diesem Fall sind die Parameter '''<span style="color: #FF7F00 ">d</span>''' und '''<span style="color:#FF7F00 ">e</span>''' ausschlaggebend für die Lage der zugehörigen Parabel. <br /> |
| | <br /> | | <br /> |
| − | *h(4) = ____________________________________________
| + | Dieses Wissen kannst du [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Wiederholung: Verschiebung von Parabeln| hier]] noch einmal auffrischen. |
| − | | + | |
| − | | + | |
| − | Wie lässt sich h(x) aus f (x) herleiten?<br>
| + | |
| − | | + | |
| − | -> h(x) = _________________________________________<br>
| + | |
| − | <br />
| + | |
| − | Für jeden x - Wert ist der Funktionswert von h gleich dem Funktionswert von f an der Stelle __________.
| + | |
| − | | + | |
| − | |}
| + | |
| − | | + | |
| − | <br>
| + | |
| − | Vergleiche deine Antworten mit der Lösung und bessere gegebenenfalls aus:<br />
| + | |
| − | | + | |
| − | {|
| + | |
| − | | + | |
| − | |width="40%"|<popup name="Graph">
| + | |
| − | [[Datei:Verschiebung nach rechts Lösung.png|400px]]
| + | |
| − | </popup>
| + | |
| | | | |
| | |width="3%"| | | |width="3%"| |
| | | | |
| − | |valign="top"|<popup name="Lösung"> | + | | [[Datei:Verschiebungen von Parabeln.png|210px|verweis=Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Wiederholung:_Verschiebung_von_Parabeln]] |
| − | Vergleiche die beiden Graphen an den vorgegebenen Werten:<br>
| + | |
| − | | + | |
| − | *h(1,5) = -3,375 = f (-1,5) = f (1,5 - 3)
| + | |
| − | <br />
| + | |
| − | *h(3) = 0 = f (0) = f (3 - 3)
| + | |
| − | <br />
| + | |
| − | *h(4) = 1 = f (1) = f (4 - 3)
| + | |
| − | | + | |
| − | | + | |
| − | Wie lässt sich h(x) aus f (x) herleiten?<br>
| + | |
| − | | + | |
| − | -> '''h(x) = f (x - 3)''' <br>
| + | |
| − | <br />
| + | |
| − | Für jeden x - Wert ist der Funktionswert von h gleich dem Funktionswert von f an der Stelle x - 3.
| + | |
| − | </popup>
| + | |
| | | | |
| | |} | | |} |
| − | <br /> | + | </td></tr></table></center> |
| − | | + | |
| − | ==== Allgemein ====
| + | |
| − | | + | |
| − | Im folgenden Applet ist die ganzrationale Funktion f: x -> x³ in schwarzer Farbe abgebildet.<br>
| + | |
| − | Verschiebe den roten Graphen der Funktion h: x -> (x - a)³, indem du über den Schieberegler den Parameter a veränderst.
| + | |
| − | | + | |
| − | Welche Auswirkungen hat eine Veränderung von a auf den Graphen von h?<br>
| + | |
| − | Was passiert, wenn a kleiner bzw. größer wird?<br>
| + | |
| − | In welche Richtung wird der Graph von h verschoben, wenn a negativ bzw. positiv ist?<br />
| + | |
| − | | + | |
| − | Vergleiche dazu die '''Wertetabelle'''!
| + | |
| − | <ggb_applet width="629" height="605" version="4.2" ggbBase64="UEsDBBQACAAIAMuitkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACADLorZCAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbOVb6W7bSBL+nXmKBn8sEkCW2QevrJyBbxmwZ4M4Gyz2xwIU2ZJ6TJEaHracmXmqeYN9sq3u5iXTVign8Q5GSOw+WN1d9dXJw6MfV4sI3fI0E0l8YOChaSAeB0ko4tmBUeTTPdf48d0PoxlPZnyS+miapAs/PzDYkBjNOhgNqS0Xi/DA8C3m+U4w3QsD191jHnX3fJuwPce2PHMS2l5AgRKtMvE2Tn7yFzxb+gG/DuZ84V8mgZ+rPed5vny7v393dzesTh8m6Wx/NpsMV1loIOA8zg6MsvMWtltbdEcVOTFNvP+vq0u9/Z6Is9yPA24gKVUh3v3wanQn4jC5Q3cizOcHhs0sA825mM1BTAczA+1LoiXIuuRBLm55BktbQyVzvlgaisyP5fVXuoeiWhwDheJWhDw9MMyh7TnMcT0PW55tU9c2UJIKHuclrVmeuV/tNroV/E5vK3vqRGZ6DqhAZGIS8QNj6kcZSCXiaQqIAkNpAcMsv4/4xE+rccMPHsA/IBCfudwLjtQwAAAOHTAycExzYFklK61zyYZDy3FzajnRHGsOzOpQ0j4U5gcwMVCcPDjRNVCeJJHaEIM60W8IGqIbitBvqmPpMSuHth46qsGmbnB50ZW/PDmwt5GmiyGthKFtYWDzgfyxnxAItw7Ve26DYK00z13Hjz1xHGvhZyJLyU1MYqKBbLBuCDS2rS+Zeg6wVQ3RDdONpWmYXs40KdM0TNMw+jUCkkpAUFgjIHGtAXasJ4XEW2myc2jtCthqKdICF5D/1U/nSLqVK3SM5xkn2uxrPP4ZBzrmmu1UhqNbXLabYPhmTI32qxg4KhlC2VzSlvaV80UmWaSesnCEkQVmbDtgkBbCHjSOjBgEYQsxC4bYRbZsHURlkGCIIhdJOkyRsmPLhV9MBRAbWbCXnHR0JEGUIYsirKyfIUABKQ8CTAgFCstCFiySp2N5LLURs2FAXcSAQek7joxjFNbBGA4niGJE5VrsIGIjmyBH+h9m0i1tV/IOmxJkm8iWS8EBwfm048EKF1EpDXjBMslEDe6cR8taKwpHES+LvMSunA8WYYVjnjwgD5Pg5qgGu7zC/Sxvk0GmavKhzlxr6fLVKPInPIKi4lpaAkK3fgT+Y6gTpkmco8oKmJ6bpf5yLoLsmuc5rMrQz/6tf+nnfHUG1Fl1tjpaZfERL4JIhMKPP4GZyC3khqhO6sRrkjpzbH1KkCRpeH2fge2g1b95mgBPmAyx6ZmUEIqZaUEtcK+vENMZutR2HY8xgplrQ/bNAl8avYWHjFBGmAWzji3z+f0Tl4ilj+a3tWj+imcV/LNUel0JrBxcZEdJ1EwtExHnx/4yL1JVoUGgTaVQh/Es4gpbFT+h1gluJsnqWoNK9V4f75dc5g/FwGR2nERJisAniZRyVrYT3SoayVlNZSoaU1GYlZZEWF/HHlEUqp3oVlGB2jVrpaS4EhOb1TEiU9FGpraWTyubkZVTEYv8shrkIrgpJcWa/qdiMQFzK5etb4m/0Zaj/QcGNsqWKffDbM55/mWTczzNF6yZHvMoum5TyiBbEVb20dodEC4WcQVQucbFm+hwTzrSk472pGM96ayedHZPOqcnnduTzuuLc2+F9NUI7qsS3FcnuK9ScF+t4L5qwX31gvsqBvfVDOmrGdLbV/pqhvTVDOmrGbJRMx+S+q6ijiLOk1SkoaJlAs54JDN1EiM0vw7SJIpUpLlt9QPFjOqm6najDO3+fVLI5A0h8yxJF0XkH7XKazl9rkJ9WQbCeKx3fUj26fHpIzgt4+l7uA+O1i5odMYgHV9fAXLqWVRP+1GU3F1DNSL86DQUeZKuX/oI9eRHscya8uaXAjofoBEpb5KvX+TJcbJYRjzn7czQyQSjG54Cw7rEiCHLF0mR6ZqnrltejYqMv/fz+WEcfuAzQP+9L0vmHNKOJm2yWQisL2Chni/Tqi9T/j8hjenZkM9SXmW/SD0u0UlXXTXbBU9nWm11liaLi/j2I9QTD1gd7VfyjLIgFUtZtqAJ1PA3LXBCkflwBxC214HwGUihbSsXuUywn0C+YC74pIBNbmH+rIhvJAGPUewHcwTlwk22n/JgnmcK87nU19V9KvwFugRW4SxfKgAK7itfQOkNoVAWgCtQQyafR+ksL/UPqlzJevb16g06QKv/vKZvFGNg8AsOVWeuKqJpESsW6/Jgqh7lSGtCyeRn8I0H5UOjGbj8RIEEprWc+/JhT+MrYJRt2NVu/5hOM56j1YGxJ2PWPbSsdfkqCdd1NRUrHj40kKbEyqFqvokBB5Vk87LiU52xCEOu7gp0PaMx6KARFwueiqAW1ldgwIFFxUgl0bYAVXWmhsjCLYxwX4yYhgg/ClEVGyP5nA0tRKwXLPyVKk38SQZRI+cQajiPmyeNmvUywGJTyifPghJ/qDVCLUf2FPQVOVil+AzO3UMRZJMipPeBcysXgRuRpUYDwc0T1zG9XroEdFTR33LMlhIfmP+BMS+tf66t//UK7SH/jfIB1MMJ5s9ygg067usHpRfYm7zgKw2+GyoOcYnWIS6DRZ9AAas6IFWPlr59qOig8HzLgbXFSkTCT+97xZKNJrzZDA9JFYV7mR2QfwHSlhDfA9MXw4VW/tkPF/pMXJ7tkS8Gzcb0c4Qf5p89+mgC+ioj2Zx/OhnmOzhef0SOu4iQ3UbkpIsI3m1ETjuIPF617QwgZx1AdtxCzjuA7HgQGXcA2fE8c0S6ecbZbUiOu5C4u43ISReRHQ+spx1Edj31dgDZcQs57wCy40Fk3AFkBxJN54HAUfVA4PUe3fiorpOo6YZEvd0D2GcxftwwTrZi/LjLuPuCfJ80fOOt+D7p8o1fkO/Thu/+PJ92eTZfkOezmuftoD7rsP2SSJ/XXG9n2Ocdrl/Srsc119vFkXGH6+8ZRjayctG5GWN/+YSwGZBOirT/+oh0LPuitmy2lWVfdCy7Qe8FHPIjX+XV+6W//VIk+d+rN9L//UOPja4MOSwy1nfoKHvthdz3fS/y6Htn9elmBlBPm28wxGd+Vf4lif6m0yy//23M5tH3sEi++7Pkl0D3MvA4/WAla7Cuv+rcBtxH3jr1AffbvVx5KXz1C3SKe7yhkrjQNXxX/QF95HXV/9tas9xP8/fyC1qNxdBxKLMch2CPeLZD9Htnc8hsz3Ut5pqEWZ4nP+P8XJcdX0aMrSF23x8x9qdHTGLjMA9+LGbazHblZ43SmoYOOKxlWhQ71CFMfsTYF7JLAbmjCo6/HuIBOiTwQwfoCPpH0D+C/jH0j6F/DP0T6J9A/wT6p9A/hf4p9M+gfwb9M+ifQ/8c+ufQH0N/DP0x/f2xXBEBA8YDbh7HGJtPo/yM7z7Ut9zqQ+Db1tfwerb5RGuvh6Ne+XkqVjWICkWJnkRNoiVRkuhIVMb49wH6VWIssZWYSiwlhhI7idmYKApaIk9LpGmJLFVIfhnKiqk/NZb77U/U1B8TlH9q+O5/UEsHCK5uRm4uCgAAGjkAAFBLAQIUABQACAAIAMuitkJFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAy6K2Qq5uRm4uCgAAGjkAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADGCgAAAAA=" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /> | + | |
| − | <br /> | + | |
| − | | + | |
| − |
| + | |
| − | <div class="lueckentext-quiz">
| + | |
| − | | + | |
| − | Allgemein gilt:<br />
| + | |
| − | Betrachtet man den Term '''f''' (x - a), wird der Graph von f um '''a''' Einheiten auf der '''x''' - Achse verschoben.<br />
| + | |
| − | Für a < 0 wird der Graph nach '''links''', für a > 0 nach '''rechts''' verschoben.
| + | |
| − | | + | |
| | </div> | | </div> |
| − | <br />
| |
| | | | |
| | + | <div style="padding:1px;background:#1C86EE;border:0px groove;"> |
| | | | |
| − | <br />
| |
| | | | |
| − | === Verschiebung nach oben/unten === | + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> |
| | + | <tr><td width="800px" valign="top"> |
| | | | |
| − | Bearbeite nun den zweiten Abschnitt auf dem Arbeitsblatt:
| + | <big>Aber auch andere Funktionsgraphen lassen sich derartig verschieben.<br> |
| − | | + | |
| − | {|
| + | |
| − | | + | |
| − | |width="40%"|[[Datei:Verschiebung nach oben.png|400px]]
| + | |
| − | | + | |
| − | |width="3%"|
| + | |
| − | | + | |
| − | |valign="top"|Vergleiche auch hier die beiden Graphen bei: <br>
| + | |
| − | | + | |
| − | *g('''-1,5''') = -1,375 = f ('''-1,5''') + ____
| + | |
| | <br /> | | <br /> |
| − | *g(0) = ______ = f (___) + ____
| + | Im Folgenden wollen wir '''allgemein''' untersuchen, welchen Einfluss Parameter in einer Funktionsgleichung auf den Verlauf des Graphens der Funktion haben.<br> |
| | <br /> | | <br /> |
| − | *g(1) = _____________________________
| + | Arbeite dich entlang des [http://wikis.zum.de/projektwiki/Datei:AB_Verschieben.pdf Arbeitsblattes] zum Thema "Verschieben von Funktionsgraphen" durch die drei Unterkapitel!</big> |
| | | | |
| − |
| |
| − | Welcher Zusammenhang besteht zwischen den beiden Funktionen?<br>
| |
| − |
| |
| − | -> g(x) = f ( ______ ) _______
| |
| − |
| |
| − |
| |
| − | Für jeden x-Wert ist der Funktionswert von g gleich dem Funktionswert von f an der Stelle ________.
| |
| − |
| |
| − |
| |
| − | |}
| |
| − |
| |
| − | Kontrolliere dein Ergebnis mit den versteckten Lösungen:
| |
| | | | |
| | {| | | {| |
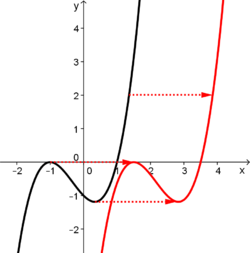
| − | | + | |valign="top"| [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- Richtung|<big><center>Verschiebung in x- Richtung</center>]] |
| − | |width="40%"|<popup name="Graph"> | + | [[Datei:Verschiebung in x- Richtung.png|250px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Verschiebung_in_x-_Richtung]] |
| − | [[Datei:Verschiebung nach oben Lösung.png|400px]] | + | |
| − | </popup>
| + | |
| − | | + | |
| | |width="3%"| | | |width="3%"| |
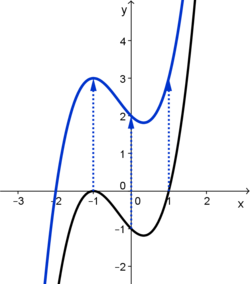
| − | | + | |valign="top"| [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in y- Richtung|<big><center>Verschiebung in y- Richtung</center>]] |
| − | |valign="top"|<popup name="Lösung"> | + | [[Datei:Verschiebung in y- Richtung.png|250px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Verschiebung_in_y-_Richtung]] |
| − | Vergleiche auch hier die beiden Graphen bei:<br>
| + | |
| − | | + | |
| − | *g(-1,5) = -1,375 = f (-1,5) + 2
| + | |
| − | <br />
| + | |
| − | *g(0) = 2 = f (0) + 2
| + | |
| − | <br />
| + | |
| − | *g(1) = 3 = f (1) + 2
| + | |
| − | | + | |
| − | | + | |
| − | Welcher Zusammenhang besteht zwischen beiden Funktionen?<br>
| + | |
| − | | + | |
| − | -> '''g(x) = f (x) + 2''' <br>
| + | |
| − | <br />
| + | |
| − | Für jeden x-Wert ist der Funktionswert von g gleich dem Funktionswert von f (x) + 2
| + | |
| − | </popup>
| + | |
| − | | + | |
| − | |} | + | |
| − | <br /> | + | |
| − | | + | |
| − | ==== Allgemein ====
| + | |
| − | | + | |
| − | | + | |
| − | | + | |
| − | Die Funktion g: x -> x³ + b lässt sich mittels des Parameters b nach oben und unten verschieben.<br>
| + | |
| − | Wenn du den Schieberegler auf b = 2 einstellst, erhälst du die obige Funktion g: x -> x³ + 2.<br>
| + | |
| − | <br>
| + | |
| − | Wie wirkt sich die Veränderung des Parameters b auf den Graphen von g aus?<br>
| + | |
| − | Was bewirkt ein positiver bzw. ein negativer Parameter b?
| + | |
| − | | + | |
| − | Beachte auch hier die '''Wertetabelle'''!
| + | |
| − | <br>
| + | |
| − | <br>
| + | |
| − | | + | |
| − | <ggb_applet width="648" height="619" version="4.2" ggbBase64="UEsDBBQACAAIAICitkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAICitkIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5Vvrbts4Fv7deQpCPxYzWF9E3d21O0jSXAZIZosmWyz2xwK0RNucyJJHohy7mLfaN9gn20NSkiXTSZWkmS6atglF6pCH5ztXUer4580yRmua5SxNJgYemAaiSZhGLJlPjILP+oHx87sfxnOazuk0I2iWZkvCJ4YzsIzdPOgNbE9MZtHEcKMAj+zQ67tTOu07M+z0ych2+pSMIp8ENArtmYHQJmdvk/RXsqT5ioT0OlzQJblMQ8LlmgvOV2+Hw7u7u0HFfZBm8+F8Ph1s8shAsPMknxjlxVtYrjXpzpbklmni4T+vLtXyfZbknCQhNZCQqmDvfngzvmNJlN6hOxbxxcTwPMdAC8rmCxDTtwIDDQXRCmRd0ZCzNc1haqMrZebLlSHJSCLuv1FXKK7FMVDE1iyi2cQwB77peL5pWyP12zdQmjGa8JLWLHkOq9XGa0bv1LLiSnJ0TDFvzXI2jenEmJE4B6lYMssAUdhQVkA359uYTklW9Xf7wT34CwTsMxVrAUsFAwDgBj1s4p5vmj3XLffSYGw9wLXs79iWAzu+Zs+suFpNrjDeg4Ge3MoeR9ABT9NYLohBn+gPBI2lGhuhP+SFq/pO2fVU15cNNlWDy5uB+DUSHe9Z0uCeXUljN6WB1Xvix7tHItzgqjRzP9N9zdX4udhu4+fcw81p4GciV8ptmZaJeqLBqrGg8Tx1y1RjgK1sLNU4qnEVjaOmO4rUUTSOonHsR8ingWpVAuIWpL7fwyPvXiHxMzVZM3UbTF1wAfFP/mgs7Ue5guaBT+AoYtPTXf4JDH3zz2A4HlYBblwaKsoXgra0HU6XuTBdeyStF2Hkgol6Phibi/AIGl9EAwthFzkudHGAPNH6yBYBwEE2CpCgwzaSNuoG8MuRwcFDLqwlBn0VJZDtINdGWFq2g8CekfQO8BTLBgrXRS5MEtyxYGt7yPGgYwfIgQ0Kv/BFjLJhHvSBuYVsjGwxF/vI8pBnIV/4FnaEy3mB2DssaiHPRJ6YCs4FjqWcCmYEyBbSgIWv0pzV4C5ovKq1InFkyargJXbleLiMKhx5ukcepeHtcQ12eYeSnDfJIA3tkp1KS61c+GYckymNoWK4FpaA0JrE4BuG5DBLE44qK3DU2DwjqwUL82vKOczK0W9kTS4Jp5szoM4r3pK1TNFjWoQxixhJPoGZiCXEgqjO2E6wy9iOV3IJ0zSLrrc52A7a/ItmqQjR/mDU+APTtuqO5VoDs/lnBKYbEmH0zqg1Z+TCpPKWa7YnVQLSdS0a2dC8gn+eCY8qgRWdX/LjNN4NrVKW8BOy4kUmyy8IopkQ6iiZx1RiK2MjFDLh7TTdXCtQbbXWzXZFRW6QG5jOT9I4zVAmJIMNz8t2qlpJI3ZWU5mSxpQUZqUlFtX38ciSFLKdqlZSgdrV1kpJcSUmNis2LJeRRKSthk9LmxFlUZEwfll1OAtvS0mxov+1WE7B3Mpp7SXxV1pyPNwzsHG+yiiJ8gWl/Msm5wdqXzBndkLj+LpJKQJoRWiV0DdWB4SLZVIBVM4J8EN0uCOd1ZHO7kjndKRzO9J5Hen8jnRBR7pRV5w7K6SrRnBXleCuOsFdlYK7agV3VQvuqhfcVTG4q2asrpqxOvtKV81YXTVjddWM9aBmPqb1A0MdRfx7qawDVDQWmTpNEFpch1kaxzLSrBvXodyMdLRMPgCWoZ1s00IkbwiZZ/DYX8TkuFE6i+FzGerLMhD6F2rVfbJPh4ePgVtOsw/wkBu3bih0LkA62p4BcqpRVA+TOE7vrqEaYSQ+jRhPs/atG6gnb9gq35U3vxdw8REaltFd8iUFT0/S5SqmnLYqEC0VjG9pBjtWNUYCab5Ii1wVPfW0N+Mipx8IXxwl0Uc6B/g/EFEzc8g7inSXziLY+xImqvEyrxKR8/8BeUyNRnSe0Sr9xfIwRGVdeddsVjzasFzqLEuXvyTrGygo9rY6HlbyjPMwYytRt6ApFPG3DXQilhN4BIia80D4HKRQxsUZFxn2E8gXLhidFrDIGsbPiuRWENAEJSRcoHRKk2GRcJpIyBdCXVfbjJEluoSNAici8Id6+4owqLwhEor6bwNKyMVZk0ryQv2gyY0oZ3/c/IQmaPPvH+2f5LbA3pcUik4uC6JZkcgN1tXBTB7TCGOCvfwGrrFXPez0ArfvqY/AslYLIg5yzNpVwCaboMvV/j6b5ZSjzcToQ9jYQoMbd6/SqK2oGdvQaN86dgUWh5r5NgEYZIrlZb0nLy5YFFH5TKCqGQWBBkZSLGnGwlrWqcQCGBbVRiqBnoaPi1WJaToNiPCDEO1AqGJfLA7J0JKBOH1YZ0k2svQg0xyiAqcQSihNdseEanNlAMWmkEAA7lryaitywEhcSXArcjA79hl8d89nD2JtPYS18C5wXukC8KSxUgIjeDqiKmjXU1cAgKzqG47X0NOegU+MeWnf84Z9o7+iqXok+4KRz59h5AeV2NnORSLdSnt/wNCfadN6MDjCJVpHuISrSyiAWRpM1blQGSx2tvH8aKDB8HTTgbnFhsWMZNtO8QI/FVsAyaoCbSfLA/IvYPo1A6wO6aNg+Uph9ATvx9G+dTCQPsu4HhlHX8C4uiPyXkcEv25ETjVEDufaVwPImQbIK7eQcw2QVx5ELjRA7NcNyLEeVb9/RLSC5NguC5K+5aP+4YJYQ87WM7RfQfe455jna9F6YC/frRofLqB0SILvHhHNsE9qww7ue9DTgNPtOvhGZv1e1+ErT+inGiLff8mnGfVpZdSd7PlUs2fz5cxZ2+v72gFxVwd8rzsg/kYOeKaZ2/fvf5oKzyoVdtbgmabBb6XAc02BrzAJnlcK7JwDzzUFfqsUeKEp8BUUdpoGLyoNQnneUYUXmgpfsjrXjzirHR/ZTzlsP7KfdYz8hPP2P+3YU4Pqhm54ddb+l9+LlP+tev/23/+ovqEjxmGS0V5BA6z1euJlj90PvmaT36nlYJWz3Qtn9pleld/Eqw/YzPJjx93LKk4y/kF8toXE2w974FrN78Fc+S7EHgRB6ysxA32us8yX4bZacM9ruIV9dof8wLF8d8i/hom+JOqO2/pCr0Qdt0f9x8Fut2Dfdkf6QDT41sa9B1jfHNgtbFzPk5g5g+BxIDktkDbdQXL+70HyBq7X9NpAOTNg57R83BROcRizYfMLCfkxa/n/WN79D1BLBwiaaWtTUgkAAHczAABQSwECFAAUAAgACACAorZC1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAICitkKaaWtTUgkAAHczAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA6QkAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
| + | |
| − | | + | |
| − | <br>
| + | |
| − | <br>
| + | |
| − | Kannst du die folgenden Graphen und Funktionsterme richtig zuordnen?
| + | |
| − | | + | |
| − | <div class="zuordnungs-quiz">
| + | |
| − | {|
| + | |
| − | | [[Datei:3x³+1.png|120px]] || f(x) = 3x³ + 1
| + | |
| − | |-
| + | |
| − | | [[Datei:X+3.png|120px]] || g(x) = x + 3
| + | |
| − | |-
| + | |
| − | | [[Datei:X² - 3.png|120px]] || h(x) = x² - 3
| + | |
| − | |-
| + | |
| − | | [[Datei:X³ + 5.png|120px]] || j(x) = x³ + 5
| + | |
| − | |-
| + | |
| − | | [[Datei:X⁴ - 2.png|120px]] || k(x) = x⁴ - 2
| + | |
| − | |}
| + | |
| − | | + | |
| − | </div>
| + | |
| − | | + | |
| − | === Verschiebung nach links/rechts und oben/unten ===
| + | |
| − | | + | |
| − | Jetzt widme dich dem dritten Abschnitt auf dem Arbeitsblatt!
| + | |
| − | | + | |
| − | {|
| + | |
| − | | + | |
| − | |width="40%"|[[Datei:Verschiebung nach rechts und oben.png|400px]]
| + | |
| − | | + | |
| | |width="3%"| | | |width="3%"| |
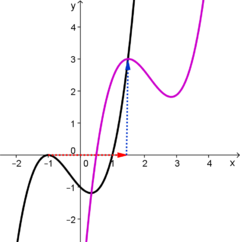
| − | | + | |valign="top"| [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- und y- Richtung|<big><center>Verschiebung in x- und y- Richtung</center>]] |
| − | |valign="top"|Die Funktion j entsteht aus der Funktion f, die um ________________ nach rechts und _________________ nach oben verschoben wird.<br> | + | [[Datei:Verschiebung in x- und y- Richtung.png|240px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Verschiebung_in_x-_und_y-_Richtung]] |
| − | Vergleiche die beiden Graphen in einem charakteristischen Punkt:<br>
| + | |
| − | <br />
| + | |
| − | *j (3) = ____ = f (0) ______ = f (___ - ___) + ___
| + | |
| − | | + | |
| − | | + | |
| − | Im Funktionsterm von j äußert sich die Verschiebung wie folgt: <br>
| + | |
| − | | + | |
| − | -> j (x) = f ( __________)__________<br>
| + | |
| − | <br /> | + | |
| − | Für jeden x-Wert ist der Funktionswert von j gleich dem Funktionswert f (_____________).
| + | |
| − | | + | |
| | |} | | |} |
| − |
| |
| − |
| |
| − | Dein Ergebnis kannst du hier überprüfen:
| |
| | | | |
| | {| | | {| |
| − | | + | {{Vorlage:Lesepfad Ende |
| − | |width="40%"|<popup name="Graph"> | + | |Link zurück=[[Manipulationen an Funktionen|Zurück zur Übersicht]] |
| − | [[Datei:Verschiebung nach rechts und oben Lösung.png|400px]] | + | |Link vor=[[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- Richtung|Los geht´s mit der Verschiebung in x- Richtung]] |
| − | </popup>
| + | |Text Copyright=<colorize>Manipulationen an Funktionen</colorize> |
| − | | + | }} |
| − | |width="3%"| | + | |
| − | | + | |
| − | |valign="top"|<popup name="Lösung">
| + | |
| − | Die Funktion j entsteht aus der Funktion f, die um 3 Einheiten nach rechts und 2 Einheiten nach oben verschoben wird.
| + | |
| − | Vergleiche die beiden Graphen in einem charakteristischen Punkt:
| + | |
| − | <br>
| + | |
| − | | + | |
| − | *j (3) = 2 = f (0) + 2 = f (3 - 3) + 2
| + | |
| − | | + | |
| − | | + | |
| − | Im Funktionsterm von j äußert sich die Verschiebung wie folgt:<br>
| + | |
| − | | + | |
| − | -> '''j(x) = f (x - 3) + 2''' <br>
| + | |
| − | <br />
| + | |
| − | Für jeden x-Wert ist der Funktionswert von j gleich dem Funktionswert f (x - 3) + 2
| + | |
| − | </popup> | + | |
| − | | + | |
| | |} | | |} |
| − | <br />
| |
| − |
| |
| − | ==== Allgemein ====
| |
| − |
| |
| − |
| |
| − | In der Funktion j: x -> (x - a)³ + b werden beide Möglichkeiten der Verschiebung zusammengeführt.
| |
| − |
| |
| − | Wie wirkt sich die Veränderung von a und b auf den Graphen der Funktion j aus?
| |
| − |
| |
| − | Kannst du eine allgemeine Regel aufstellen?
| |
| − |
| |
| − | <ggb_applet width="737" height="619" version="4.2" ggbBase64="UEsDBBQACAAIAC6ltkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAAupbZCAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1b21LbSBq+zjxFly62klpsq3W0s3amgEAglcymQja1tRdb1ZbadgdZ8kgtMKl5q3mDebL9+6CDETFtyCwZk0C7W38fvu8/SoLxz+tlgq5oXrAsnVi4b1uIplEWs3Q+sUo+6w2tn1/9NJ7TbE6nOUGzLF8SPrG8vmM186DXdwMxmcUTa2TblEy9US+a+WHPm2HSI7YT96gdUJuM3NgPphZC64K9TLNfyJIWKxLRi2hBl+RdFhEu11xwvno5GFxfX/er3ftZPh/M59P+uogtBCdPi4mlP7yE5TYmXbtS3LFtPPj3+3dq+R5LC07SiFpIoCrZq5+eja9ZGmfX6JrFfDGxQt+10IKy+QJghs7QQgMhtAKsKxpxdkULmNrqSsx8ubKkGEnF9WfqE0pqOBaK2RWLaT6x7H5o45Hj2mGgf1ooyxlNuZa19Z6DarXxFaPXalnxSe7o2aMQVMAKNk3oxJqRpABULJ3lwCgcKC+hW/CbhE5JXvWb8+AD+AcC7CsVa8GWioaJ5QfOAcbhQWjbB76vz9La2Nmyq+432+qBZl/7wK52ddq7wvgBDBzIo9zaEXTAsyyRC2LQJ/oNQeOoxkXoN/nBV31PdwPVDWWDbdVgfXEofoxEJ3gUGnzgVmjcNhpY/UB8B99AhFu7Ks3sQmG1pY/xJoHeN7bzWgTayJfAHdux0YFosGocaIJAXbLVGJArG0c1nmp8JeOp6Z4S9ZSMp2Q89zEAnQogth0zgPiRaqw39NuOAPYv/svvzpbuTn7Qcb8H7Bh4j/H3B2wY2ht2UxmNarFut9Hw3Q41HlQRcKwPhIqFkNW2xemyEEd0R9K6EUY+mHAQgjH6CI+gCUW4cBD2kedDFw9RINoQuSJCeMhFQyTksIukDftD+OHJ6BEgH9YSg6EKI8j1kO8iLC3fQ8ACkt4DnDguSPg+8mGS2B2Lbd0AeQF03CHy4IDCb0IRxFyYB33Y3EEuRq6Yi0PkBChwUCh8D3vCJYOhODss6qDARoGYCs4HjqecDmYMkSvQgBessoLV5C5osqq1Inlk6arkmjs9Hi3jikee3RKPs+jyqCZbX6Gk4G0xyFNNNlR5ayNZPhsnZEoTKCkuhCUgdEUS8B9L7jDLUo4qK/DU2DwnqwWLigvKOcwq0BdyRd4RTtenIF1Ue8utZQ4f0zJKWMxI+hnMRCwhFkR1SnfDJqV7w5HaJcqyPL64KcB20Po/NM8g8Izs/qj1BYnnRl/x/Y0rIvcWERFG7402r4hJ37ikd6ZXNTKypkXF/jwXTqd5FZ3z4ihLmqFVxlJ+TFa8zGV5BjE2F5gO03lCJbUydEKhE11Os/WF4tRVa326WVGROuQBpvPjLMlylEtgIKDbqWqljDhZLWVLGVtK2JWSWFxfh3JGSsh2qlopBVpXR9NIcQUT29U2rJDBRmS1lktLkxFlU5ky/q7qcBZdaqRYyf9SLqdgbXra5pL4Oy05Htyyr3GxyimJiwWl/H6LG2qoMGd2TJPkoi2J3aCRdDT3reWB4nKZVgxVk+ytgrgWDO1tco6hnGso5xnK+YZygaFcaCg3NJQbGcph21TQVCPYVCXYVCfYVCnYVCvYVC3YVC/YVDHYVDOOqWYcY18x1YxjqhnHVDPOVs18zOpbijqMhN+UchopV2fggiYiVWcpQouLKM+SRIaaq+ozHDOSh5HDuYinVXAnN1kpsjcEzdMsX5YJOWrV12L4jQz2ug6E/pla9bbY57uHj2C3guYf4DY42big2DkDdHRzBuBUo6geJkmSXV9AOcJIchIznuWblz5BQfmJrYqmvvm1hA8foWE5bdIvKXl2nC1XCeV0owTpJIPxJc3hxKrISCHRl1lZqKqnnvZsXBb0A+GLwzT+SOdA/wciimYOmUeJNgkthrMvYaIa1+QTkfX/BZlMjcZ0ntMqASbycYnKu/Kq3S55OsNyqdM8W56nV5+gpLh11PGgwjMuopytROWCplDFX7bYiVlB4B4gbs8D8AWgUMbFGRc59jPgixaMTmmKrmD4tEwvxXXopiRaICgYLotBTqMFLyBRxygDyUGZcppKFSyE+t7f5Iws0Ts4OOxMuHyYgN4TBqU4REZREK5BKYV4OqXSvjAH0Oxa1LfP1y/QBK3/+9x9IY8J9r+kUIVyWSLNylQeuK4XZvLBjjAuOMsXcJVb9USjJ7j8jYoJLG21IOLRj127DthoWwlytX/OZgXlaC3d+WZi9Uati++zeFNvM7am8W1jaSouDjX0ZQosyIzLdQEoP5yxOKbyHkGVN4qBDhdpuaQ5i2qoRFIBG5bVQSo8u9JTlZ2KIB+3GMJbGWpI0HJFIp6qoSUDOD2IVUuyljGLTAsIEpxCZKE0bZ4rqsPVhZRAIPgOsC8+3YgcHIpPktxKHKyOfQVXNqDa2Ua18DVwZekQcOOxUngR3CxRFcLrqSvAL6v8lhuaqmn63dSkrFioR9wa2N4PoKahVpPjuVvV1Iq0T6inW2FoYi10FFqoKPR8jXqIvJCxCBkEo8U9waiF2tDdTANSz9EhqbpLvzsm3cm1WxHm3Bt/OoR90YR96RCG/o6mRqR9eVAEl+Zec7Zp/Oak2Zq0u51jG2nmMbvD2VxzNm+lOmO25g8zsS2hwpwtR7P1f7WwT3TNsWbsb7+WGf+HKBEm6z9+V707igQOU6zN+Y8gbdcqwawQkE/WoHpms6ZCZl/pe/2aTz1ys/Xj2Sbu3RmPkYy9OgJ4nhmnzganm/77x+/CHs35dR4Y9x7sw0/GsQoYYXgfx1DRHlZWe4i1o5vUs4d32Gr1RuTJjJWUa5Ywkt8YlbNbc/d2wzysrHJmFAwPH2h4+8GVW+VeM67cH9NJ/yy+ttbgR/h2Ed7z7qzCH+V6Oxbhu9BjDvW4C9XdU6ivu1CdPYV60oWK9xTqaQfq3TfMf32kbzpI91WnZx2k++qo5x2k+xp933aQ7mtKPXI6wTfYV6zHXazyCew+Yn3dxTrcU6gnXaj7mmtOO1D3tn7oIN1XnZ51kO6ro553kO5t+H3bgfpXzqqd5zVH1fOa5z3v3rcknZLD3VJymD6u+e6QjhtI7s6QjruQGtN+MkivG0jOzpBedyENnxzRSYMI74zopIsIPzmi0wbRbmhOO2jsJwfzpgazu3bedPA8vXLOajy7+89ZB8/Tu8/bGs/uUfttB88PELTPa0C7x+zzDqAfIGSLN5DuxtvMG/NXlw98K/JnvkEqOMn5B/HnBPKlY8/ue3jjjxuG6kVvfwi0fq19/n6SvA2S1uYkeT88ScN+YLe/fPWrCkCd0x4Wv8F9N2OD9q9Dyj9d0X/W+up/UEsHCAQhYtG2CQAAhjsAAFBLAQIUABQACAAIAC6ltkJFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgALqW2QgQhYtG2CQAAhjsAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAABOCgAAAAA=" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
| |
| − |
| |
| − | <br />
| |
| − | <br />
| |
| − |
| |
| − | Fülle den Lückentext mit den vorgegebenen Antwortmöglichkeiten aus.<br />
| |
| − | Ergänze anschließend die Lücken im Merksatz auf deinem Arbeitsblatt.<br />
| |
| − |
| |
| − |
| |
| − | <div class="lueckentext-quiz">
| |
| − | Allgemein gilt:<br />
| |
| − | Betrachtet man den Term '''f'''(x - a) + b, wird der Graph von f um '''a''' Einheiten auf der x - Achse und um '''b''' Einheiten auf der y - Achse verschoben.<br />
| |
| − | Für a < 0 wird der Graph nach '''links''', für a > 0 nach '''rechts''' verschoben.<br />
| |
| − | Der Parameter b < 0 verschiebt den Graphen nach '''unten''', b > 0 nach '''oben'''.
| |
| − |
| |
| − | </div>
| |