Achtung:

Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.

Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.

Gerne kannst Du natürlich weiterarbeiten

im neuen Projektwiki (projekte.zum.de).

Verschieben von Funktionsgraphen: Unterschied zwischen den Versionen

Aus Projektwiki - ein Wiki mit Schülern für Schüler.
Wechseln zu: Navigation, Suche
K
 
(28 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 
__NOTOC__
 
__NOTOC__
−
In der neunten Klasse lernst du, wie sich Parameter auf die Graphen von Parabeln auswirken können.
+
<div style="padding:1px;background:#1C86EE;border:0px groove;">
  
−
Auch andere Funktionsgraphen lassen sich derartig verschieben. <br>
+
 
−
Im folgenden wollen wir untersuchen, welchen Einfluss Parameter in einer Funktionsgleichung auf den Verlauf des Graphens der Funktion haben.
+
<center><table border="0" width="800px" cellpadding=5 cellspacing=15>
−
<br>
+
<tr><td  width="800px" valign="top">
−
Arbeite dich entlang des Arbeitsblattes zum Thema "Verschieben von Funktionsgraphen" durch die 3 Unterkapitel!
+
{|
−
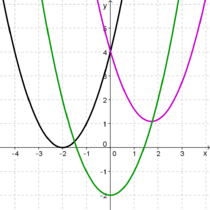
#[[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- Richtung|Verschiebung in x- Richtung]]
+
| valign="top"|In der 9. Klasse lernst du, welchen Einfluss die Parameter '''<span style="color: #FF7F00  ">a</span>''', '''<span style="color:#FF7F00  ">b</span>''' oder '''<span style="color:#FF7F00  ">c</span>''' auf eine Parabel, also auf den Graphen einer quadratischen Funktion mit dem Funktionsterm<br />
−
#[[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in y- Richtung|Verschiebung in y- Richtung]]
+
f (x) = '''<span style="color:#FF7F00 ">a</span>'''x<sup>2</sup> + '''<span style="color: #FF7F00  ">b</span>'''x + '''<span style="color: #FF7F00  ">c</span>''',<br />
−
#[[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- und y- Richtung|Verschiebung in x- und y- Richtung]]
+
haben.<br />
 +
<br />
 +
Oft wird auch die Scheitelform einer quadratischen Funktion<br />
 +
f (x) = (x - '''<span style="color:#FF7F00  ">d</span>''')<sup>2</sup> + '''<span style="color: #FF7F00 ">e</span>'''<br />
 +
betrachtet.<br />
 +
In diesem Fall sind die Parameter '''<span style="color: #FF7F00 ">d</span>''' und '''<span style="color:#FF7F00 ">e</span>''' ausschlaggebend für die Lage der zugehörigen Parabel. <br />
 
<br />
 
<br />
−
Damit sammelst du das ganze Wissen über das Verschieben von Funktionen, das du auch im Abitur gut gebrauchen kannst.
+
Dieses Wissen kannst du [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Wiederholung: Verschiebung von Parabeln| hier]] noch einmal auffrischen.
−
<br>
+
−
[[Datei:AB Verschieben.pdf]]  
+
−
<br>
+
  
 +
|width="3%"|
  
 +
| [[Datei:Verschiebungen von Parabeln.png|210px|verweis=Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Wiederholung:_Verschiebung_von_Parabeln]]
  
 +
|}
 +
</td></tr></table></center>
 +
</div>
  
−
Zuvor kann eine kurze Wiederholung nützlich sein:
+
<div style="padding:1px;background:#1C86EE;border:0px groove;">
  
−
=== Wiederholung: Verschiebung von Parabeln ===
 
  
−
Im folgenden Applet kannst du über die Funktionen h bzw. g die Verschiebung nach links/rechts (durch den Schieberegler a) bzw. nach oben/unten (durch den Schieberegler b) beobachten.<br>
+
<center><table border="0" width="800px" cellpadding=5 cellspacing=15>
−
Klicke auf die jeweiligen Checkboxen im Applet, um die Funktionen anzuzeigen oder auszublenden.
+
<tr><td  width="800px" valign="top">
  
−
In der Funktion j werden beide Arten der Verschiebung zusammengeführt.
+
<big>Aber auch andere Funktionsgraphen lassen sich derartig verschieben.<br>
 +
<br />
 +
Im Folgenden wollen wir '''allgemein''' untersuchen, welchen Einfluss Parameter in einer Funktionsgleichung auf den Verlauf des Graphens der Funktion haben.<br>
 +
<br />
 +
Arbeite dich entlang des [http://wikis.zum.de/projektwiki/Datei:AB_Verschieben.pdf Arbeitsblattes] zum Thema "Verschieben von Funktionsgraphen" durch die drei Unterkapitel!</big>
  
−
<ggb_applet width="1029" height="619"  version="4.2" ggbBase64="UEsDBBQACAAIAFintkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAFintkIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVltbxs3Ev6c/orBfigSnCXxbd9yUoq2QHEFnDao06LohyuoXUqivdrV7VKyHORX9Sf0l92Q3JVWdqyTawXXODbF5XCG88zMw1l7/NV2WcBG1Y2uyklAhyQAVWZVrsv5JFib2SAJvnrzxXiuqrma1hJmVb2UZhKIIQv2+3A25JHdrPNJkCk2UyIhA5nLeCBmeTZIUh4NYjFLWBopFk6zAGDb6Ndl9YNcqmYlM3WVLdRSXlaZNE7nwpjV69Ho9vZ22FkfVvV8NJ9Ph9smDwBPXjaToP3wGtUdbLrlTpwRQke/vr306ge6bIwsMxWA9Wqt33zxYnyry7y6hVudmwViQEQYwELp+QL9jFkSwMhKrdDZlcqM3qgG9/amzmmzXAVOTJZ2/YX/BMXOnwByvdG5qicBGTLBKAlZxGkYJ6mIRQBVrVVpWmHaGh116sYbrW69XvvJmRQkjTEIutHTQk2CmSwa9EuXsxoxxRPVa5w25q5QU1l38/2B6AV+oYD+oKwuDJ4HYhJEQlzQiF/EhFyEIfFn6RsOwFRV4bQSCFP4+BEYYQQu7ED9wHCIIr9E/DPC/cD8IPwQehnhtwsvKryM8DKCH/Gzne8dbR8ceNr5yfp+kgtygY5fOOfv+Zj0fKTWgY9A7cndwMGembqz20G008hPYzdQ4gfaLib2h8Mqeoo3D8PGO2d43xlUfmG/o0ccoj2jXucTbHYWKWHpafixZ0WMPxov9ph7TwL1YYrsPAx7BkPMf/vffT8wyZ/k4+OYnm4xEs+p979gMCYHpd7VuR9pOx6D4WyHGo86Bhy3B4JmYWXbXDZq2dgj8tQRElAIsWijGPkjBJriENviZUBDECFOaQKRHWPgtl4FcEjAylEOjnbCBH8IV8sRhKjLPox9UQMXEHKgjqwEIArgCA8xYRwlwhBC3GStU2uWRyAinPAEBB7QUl1sKYXjPpyjcQacArd7aQwsgohBbOmSCsuiUWLPjkoZRAQiuxX5ErnS8yTuSIBbb7AKVlWjd+AuVLHaRcXhqMvV2rTYtc+zZd7haKp74nmV3XyzA7tdUbIxfTG8p/bXob+3Dm7LF+NCTlWBTcWVzQSAjSxskTsLs6o00GWB8M/mtVwtdNZcKWNwVwPXciMvpVHb71C66Ww70+4WH6t1Vuhcy/IXTBOrwiqE/aVueau71MOUejNZVdX51V2DyQPb31Rd4d0msI9haZKyMKJpwkNE9M4vcZIO45SRtP3CK6LJpM36iAxF2vuH1/Ldfin0xtRm543cqqZDfF7bQmuxtJPvm2+qYv9oVenSfCtXZl27pgypsbZufF3OC+XgdGSL7U12M622Vx5H7nW9v1vhjPgDTOffVkVVA5YhC7HHmbfj1I9Oxp5sJ0WcDHESpAuMznfrNGVOwo1TPzopjLQ/Wusp7dykpDOjG0cwqLxfxi5NbK+0LrW57CZGZzetp9TL/7BeTjHD2m2HKumZVI5H93JqfKPqUhU+cUqM5LpaNz6Vd+n4Yrxu1DtpFl+X+U9qjmX4TlomNKjai+5PnKtML3Gjf95CJ21Yf8aj+qe5mteq87BwXbAH1q2Sfho/eOxUfVdXy+/LzXvMmXtHHY86f8ZNVuuVTU2YIjXfqH325bqRSOx5fx8636AXmSUZBNJYEH9B/7KFVtM1Ktngc+s2Yl0GINdmUWG2vL2rtVzCJR4L9WIto88M3kqN7In5amt4u6pVY18pfNQArSLZbC0lvdy+ggls//2SvXKHUIVaYr8MxmX4bF264+zCPXPNuI0rVNNrJKJ76bCPAi4/kvAgi9VC2na9BbSQd6o+gNhp+3E2a5SBrdtzZxNqv/a2ytUh2+mtyu9nwr5eDLLeDbb8mIdYmaYtX/fhXzrPVdmqx+T0ADyAolwvVa2znafSIYEG1112dO48FZ2ONDw+Ie0BRI8CtAehlWsK+yIES43uDLCnWcqte6uQ06Yq1gbfBTHpy/27oD/cjsutBxbuJEmHLeRxaD85cDtxTDr9Aev0BKjZMahtIWGdumzHm2Ll/QW83pRnm93WFfrvOLpXY6eGaXq2MPkktuGxxE7EyWHa53FyJI/PHMKUtiFkKTkawh7F/h9jeI+hJsF7tTW0Jakv/7OuzD87qvrzDz//BF1hH2OCQw3HI91z/vl8tY8lOcJJnw4k2KClJHQhE+x4jk+xUVdyT8rZ7/R+lvccO2Oen8rXSUKdI0l4DJ6utTrITb+CbZkFxUnPd3GHf8D0acjkZ8TlCE2fjouvyVCcAZeFx+XlFgYgX/35x9OQUedExibJDpm/mjLMkyONzoDN9T1sPpk5Dzhn0fLNIbKuNYITeqPFyb0Rdnq59qSJ0j+2wvlnybkBjf09cLR9eman9ADKeQvlvNdfuiCcAuT8mUBaPvwctDZg7H83oudG8rpF8vpBUp6M5/Uz8fxMJS98Xn76Cv1MaNqmgB20FXendxPs79dNNEbW5p39VYbrIAZkyKkIBY/iJKZExG3GimHCOCFpHMUkZQKL4IP/q9RJgPEDwLanA8b/9oClQ05CllLCGeH2n4PLwohIxSyJ45CHUZIy/hhko/5ru/u9WftXtTf/BVBLBwi9RnxEkwcAAAUcAABQSwECFAAUAAgACABYp7ZC1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAFintkK9RnxEkwcAAAUcAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAKggAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
 
−
<br>
 
−
<br>
 
  
 +
{|
 +
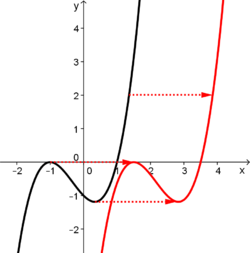
|valign="top"| [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- Richtung|<big><center>Verschiebung in x- Richtung</center>]]
 +
[[Datei:Verschiebung in x- Richtung.png|250px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Verschiebung_in_x-_Richtung]]
 +
|width="3%"|
 +
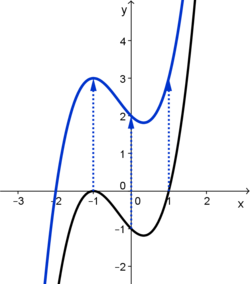
|valign="top"| [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in y- Richtung|<big><center>Verschiebung in y- Richtung</center>]]
 +
[[Datei:Verschiebung in y- Richtung.png|250px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Verschiebung_in_y-_Richtung]]
 +
|width="3%"|
 +
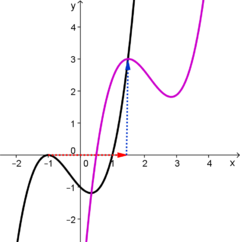
|valign="top"| [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- und y- Richtung|<big><center>Verschiebung in x- und y- Richtung</center>]]
 +
[[Datei:Verschiebung in x- und y- Richtung.png|240px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Verschiebung_in_x-_und_y-_Richtung]]
 +
|}
  
−
<popup name="Extra-Aufgabe">
+
{|
−
<div class="multiplechoice-quiz">
+
{{Vorlage:Lesepfad Ende
−
 
+
|Link zurück=[[Manipulationen an Funktionen|Zurück zur Übersicht]]
−
Wie wirken sich die beiden Parameter a und b auf den Scheitelpunkt S(x<sub>0</sub>/y<sub>0</sub>) von j: x -> (x - a)² + b aus?
+
|Link vor=[[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- Richtung|Los geht´s mit der Verschiebung in x- Richtung]]
−
(!S(-a/-b))  (S(a/b)) (!S(-a/b)) (!S(a/-b))
+
|Text Copyright=<colorize>Manipulationen an Funktionen</colorize>
−
 
+
}}
−
</div>
+
|}
−
</popup>
+

Aktuelle Version vom 15. August 2013, 15:43 Uhr


In der 9. Klasse lernst du, welchen Einfluss die Parameter a, b oder c auf eine Parabel, also auf den Graphen einer quadratischen Funktion mit dem Funktionsterm

f (x) = ax2 + bx + c,
haben.

Oft wird auch die Scheitelform einer quadratischen Funktion
f (x) = (x - d)2 + e
betrachtet.
In diesem Fall sind die Parameter d und e ausschlaggebend für die Lage der zugehörigen Parabel.

Dieses Wissen kannst du hier noch einmal auffrischen.

Verschiebungen von Parabeln.png


Aber auch andere Funktionsgraphen lassen sich derartig verschieben.

Im Folgenden wollen wir allgemein untersuchen, welchen Einfluss Parameter in einer Funktionsgleichung auf den Verlauf des Graphens der Funktion haben.

Arbeite dich entlang des Arbeitsblattes zum Thema "Verschieben von Funktionsgraphen" durch die drei Unterkapitel!


Verschiebung in x- Richtung

Verschiebung in x- Richtung.png

Verschiebung in y- Richtung

Verschiebung in y- Richtung.png

Verschiebung in x- und y- Richtung

Verschiebung in x- und y- Richtung.png

Zurück zur Übersicht Los geht´s mit der Verschiebung in x- Richtung

Manipulationen an Funktionen

Von „https://projektwiki.zum.de/index.php?title=Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen&oldid=3508“