Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Benutzer:Valentin WWU3: Unterschied zwischen den Versionen
| (30 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == | + | ==Über mich== |
| − | + | *Seminar: [[Digitale Werkzeuge in der Schule|Wikiprojekt zu dem Seminar "DiWerS]] | |
| − | + | *Projekt: [[Digitale_Werkzeuge_in_der_Schule/Trainingsfeld_Ableitungen|Trainingsfeld Ableitungen]] | |
| + | *betreut von: [[Benutzer:Elena Jedtke|Elena Jedtke]] | ||
| + | ==Aufgabe 5: Ein Tag im Zoo== | ||
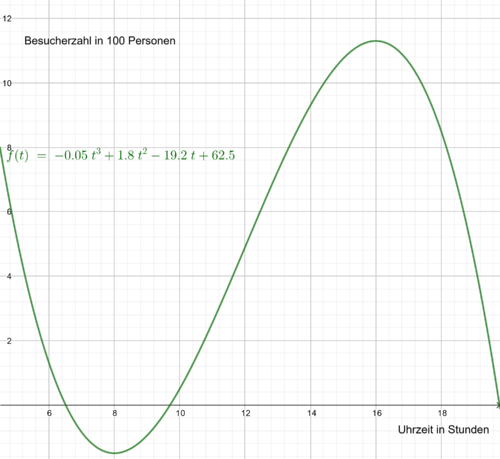
| − | + | {{Aufgaben| 5 : Ein Tag im Zoo}} Ein Zoo ist bekanntermaßen in den Sommerferien am besten besucht. Die Besucherzahlen eines bestimmten Zoos (in 100 Personen) kann durch die Funktion b(t) = - 0,05 t³ + 1,8 t² - 19,2 t + 62,5 für 10 < t ≤ 19,5 näherungsweise beschrieben werden. Dabei gibt ''t'' die Uhrzeit in Stunden an.<br /> <br /> | |
| − | {{ | + | [[Datei:Besucherzahlen2.png|500px|zentriert|thumb|Abb. 5.1: Besucherzahl eines Zoos]] <br /> |
| − | + | Die Lösungen musst du per Hand ausrechnen und kannst sie anschließend mit diesen vergleichen. <br /> | |
| − | + | '''a)''' Zu welcher Uhrzeit befinden sich am meisten Besucher in dem Zoo? Und wie viele sind es?<br/> | |
| + | <popup name="Tipp">Die Ableitung lautet: b´(t) = - 0,15 t² + 3,6 t - 19,2 </popup> | ||
| + | <popup name="Lösung">Die Nullstellen der Ableitung entsprechen den Maximalstellen der Normalfunktion. Setzt man die Ableitung gleich 0, also 0 = b´(t) = - 0,15 t² + 3,6 t - 19,2 , dann erhält man t_1 = 8 und t_2 = 16. Da der Zoo erst um 10:00 Uhr (also t = 10) öffnet, ist t_2 die einzige Lösung. <br/> Setzt man das in die Funktion ein erhält man: b(16) = 11,3 . <br/>'''Die Antwort: Mit 1130 Besuchern sind um 16:00 Uhr die meisten Menschen im Zoo.</popup> | ||
| + | <br/> | ||
| + | '''b)''' Wann ist die Besucherzahl am geringsten? Und warum ist es falsch, an dieser Stelle nach der Minimalstelle zu suchen? <br/> | ||
| + | <popup name="Tipp">Bei dieser Aufgabe ist es wichtig, sich den Definitionsbereich noch einmal genauer anzugucken. Du darfst auch mit der Abbildung 5.1 deine Begründung unterstützen.</popup> | ||
| + | <popup name="Lösung">Die Besucherzahl ist um 19:30 Uhr am geringsten. Das ist der einzige Nullpunkt im Definitionsbereich. Die Minimalstelle liegt, wie man in der Abbildung deutlich erkennen kann unterhalb der x-Achse und eine negative Besucherzahl ist nicht möglich. Außerdem liegt diese Stelle nicht mehr im Definitionsbereich.</popup> | ||
| + | <br/> | ||
| + | '''c)''' Zu welcher Uhrzeit ist der Andrang in den Zoo am größten? <br/> | ||
| + | <popup name="Tipp 1">Mit der Frage nach dem größten Andrang ist der größte Zuwachs an Besuchern gemeint.</popup> | ||
| + | <popup name="Tipp 2">Die zweite Ableitung lautet: b´´(t) = - 0,3 t + 3,6</popup> | ||
| + | <popup name="Lösung">Indem die zweite Ableitung gleich 0 gesetzt wird, kann man die Wendestelle ausrechnen. Daraus ergibt sich t = 12. Also sind die meisten Menschen um 12:00 Uhr auf den Weg in den Zoo.</popup><br /> | ||
| − | {{ | + | <br /> }} |
| + | ==Aufgabe 6: Die Autofahrt== | ||
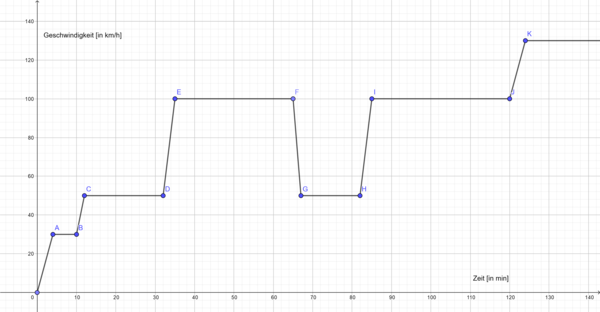
| + | {{Aufgaben| 6 : Die Autofahrt|Familie Müller fährt zusammen in den Urlaub. Der Sohn Peter möchte gerne wissen, wie weit sie insgesamt gefahren sind. Dazu hat er die Geschwindigkeit des Autos zu bestimmten Zeitpunkten auf der Anzeige im Auto abgelesen und sich notiert. Die Geschwindigkeit könnte man in einem Graphen darstellen, wie in Abbildung 6.1. <br/> | ||
| + | [[Datei:Geschwindigkeitsnotizen1.png|600px|zentriert|thumb|Geschwindigkeitsprofil einer Urlaubsfahrt]]<br /> | ||
| − | + | '''a)''' Fülle die Lücken mit den richtigen Antworten.<br /> | |
| + | <iframe src="https://learningapps.org/watch?v=phzt4r2ba18" style="border:0px;width:80%;height:400px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> <br /> | ||
| − | |||
| − | + | '''b)''' Was passiert in den Zeiträumen, in denen die Geschwindigkeit nicht konstant sind? <br /> | |
| − | + | <popup name="Lösung">Wenn der Graph fällt, sinkt somit die Geschwindigkeit. Also wird das Auto gebremst. <br/> Steigt der Graph, so steigt auch die Geschwindigkeit und der Fahrer beschleunigt.</popup> <br /> | |
| − | + | '''c)''' Wie viele Kilometer ist das Auto von Peters Familie in dem Zeitraum von Minute 67 bis Minute 82 gefahren? | |
| + | Schreibe die Lösung in dein Heft. <br /> | ||
| + | <popup name="Tipp 1">Beachte die Einheiten. Die Fahrtzeit ist in Minuten [min] angegeben und die Geschwindigkeit in Stundenkilometer/Kilometer pro Stunde [km/h].</popup> | ||
| + | <popup name="Tipp 2">Wie lang ist die Zeit zwischen Minute 67 bis Minute 82? Rechne diese Differenz von Minuten [min] in Stunden [h] um.</popup> | ||
| + | <popup name="Tipp 3">In dem Zeitraum liegen 15 Minuten, die entsprechen 1/4 Stunde. Wenn man 15 Minuten, also eine Viertelstunde, mit einer Geschwindigkeit von 50 km/h fährt. Wie viel Strecke hat man dann zurückgelegt?</popup> | ||
| + | <popup name="Lösung">Von Minute 67 bis Minute 82 ist eine Viertelstunde vergangen, in der die Familie 12,5 km zurückgelegt hat.</popup> <br /> | ||
| − | + | '''d)''' Wie viele Kilometer hat Peters Familie in den ersten 2 Stunden näherungsweise zurückgelegt? | |
| − | + | ||
| − | < | + | "Näherungsweise" bedeutet an dieser Stelle musst du nur die Phasen konstanter Geschwindigkeit in Betracht ziehen. Schreibe die Lösung in dein Heft.<br /> |
| + | <popup name="Tipp">Wenn man die Beschleunigs- und Bremsphasen beiseite lässt, erhählt man fünf einzelne Abschnitte, die man wie in Aufgabe '''c)''' berechnen kann. (Zeit*Geschwindigkeit=Strecke)</popup> | ||
| + | <popup name="Lösung"> Strecke AB (6 Minuten): 0,1 h * 30 km/h = 3 km <br/> Strecke CD (20 Minuten): 0,333 h * 50 km/h = 16,666 km <br/> Strecke EF (30 Minuten): 0,5 h * 100 km/h = 50 km <br/> Strecke GH (15 Minuten): 0,25 h * 50 km/h = 12,5 km (siehe '''c)''') <br/> Strecke IJ (35 Minuten): 0,583 h * 100 km/h = 58,33 km <br/> '''Insgesamt also:''' 3 km + 16,66 km + 50 km + 12,5 km + 58,33 km = 140,5 (Rundungsfehler sind hier möglich!)</popup> | ||
| + | <br /> | ||
| + | '''e)''' Wir nehmen an, der abgebildete Graph beschreibt die Ableitung einer Funktion. Was gibt dann die Funktion an und wovon ist sie abhängig? | ||
| + | |||
| + | Schreibe die Lösung in dein Heft.<br /> | ||
| + | <popup name="Tipp">Betrachte die vorherigen Aufgaben und ihre Ergebnisse noch einmal.</popup> | ||
| + | <popup name="Lösung">Wenn die Ableitung die Geschwindigkeit in Abhängigkeit von der Zeit angibt, dann gibt die Funktion die Strecke in Abhängigkeit von der Zeit an.</popup> <br /> | ||
| + | |||
| + | '''f)''' Berechne die durchschnittliche Geschwindigkeit, die Peters Familie in den ersten zwei Stunden gefahren ist.<br /> | ||
| + | <popup name="Lösung">Die durchschnittliche Geschwindigkeit ergibt sich durch die gefahrene Strecke dividiert durch die Zeitspanne (2h). Aus Aufgabenteil '''d)''' kennen wir die gefahrene Strecke näherungsweise: | ||
| + | <br/>Also: '''140,5 km / 2 h = 70,25 km/h''' | ||
| + | <br/>''Auch hier kann dein Ergebnis abweichen, wenn du in '''d)''' ein anderes Ergebnis berechnet hast''</popup>}} | ||
Aktuelle Version vom 12. Januar 2019, 22:49 Uhr
Über mich
- Seminar: Wikiprojekt zu dem Seminar "DiWerS
- Projekt: Trainingsfeld Ableitungen
- betreut von: Elena Jedtke
Aufgabe 5: Ein Tag im Zoo
|
{{{2}}} |
Die Lösungen musst du per Hand ausrechnen und kannst sie anschließend mit diesen vergleichen.
a) Zu welcher Uhrzeit befinden sich am meisten Besucher in dem Zoo? Und wie viele sind es?
b) Wann ist die Besucherzahl am geringsten? Und warum ist es falsch, an dieser Stelle nach der Minimalstelle zu suchen?
c) Zu welcher Uhrzeit ist der Andrang in den Zoo am größten?
}}
Aufgabe 6: Die Autofahrt
|
Familie Müller fährt zusammen in den Urlaub. Der Sohn Peter möchte gerne wissen, wie weit sie insgesamt gefahren sind. Dazu hat er die Geschwindigkeit des Autos zu bestimmten Zeitpunkten auf der Anzeige im Auto abgelesen und sich notiert. Die Geschwindigkeit könnte man in einem Graphen darstellen, wie in Abbildung 6.1. a) Fülle die Lücken mit den richtigen Antworten.
c) Wie viele Kilometer ist das Auto von Peters Familie in dem Zeitraum von Minute 67 bis Minute 82 gefahren? Schreibe die Lösung in dein Heft. d) Wie viele Kilometer hat Peters Familie in den ersten 2 Stunden näherungsweise zurückgelegt? "Näherungsweise" bedeutet an dieser Stelle musst du nur die Phasen konstanter Geschwindigkeit in Betracht ziehen. Schreibe die Lösung in dein Heft.
Schreibe die Lösung in dein Heft. f) Berechne die durchschnittliche Geschwindigkeit, die Peters Familie in den ersten zwei Stunden gefahren ist. |