Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Benutzer:Valentin WWU3: Unterschied zwischen den Versionen
| (10 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | ==Aufgabe 5: | + | ==Über mich== |
| − | {{Aufgaben|5: | + | *Seminar: [[Digitale Werkzeuge in der Schule|Wikiprojekt zu dem Seminar "DiWerS]] |
| − | [[Datei:Besucherzahlen2.png| | + | *Projekt: [[Digitale_Werkzeuge_in_der_Schule/Trainingsfeld_Ableitungen|Trainingsfeld Ableitungen]] |
| + | *betreut von: [[Benutzer:Elena Jedtke|Elena Jedtke]] | ||
| + | |||
| + | ==Aufgabe 5: Ein Tag im Zoo== | ||
| + | |||
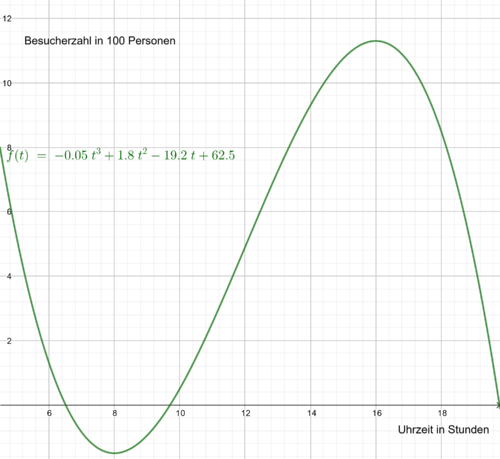
| + | {{Aufgaben| 5 : Ein Tag im Zoo}} Ein Zoo ist bekanntermaßen in den Sommerferien am besten besucht. Die Besucherzahlen eines bestimmten Zoos (in 100 Personen) kann durch die Funktion b(t) = - 0,05 t³ + 1,8 t² - 19,2 t + 62,5 für 10 < t ≤ 19,5 näherungsweise beschrieben werden. Dabei gibt ''t'' die Uhrzeit in Stunden an.<br /> <br /> | ||
| + | [[Datei:Besucherzahlen2.png|500px|zentriert|thumb|Abb. 5.1: Besucherzahl eines Zoos]] <br /> | ||
Die Lösungen musst du per Hand ausrechnen und kannst sie anschließend mit diesen vergleichen. <br /> | Die Lösungen musst du per Hand ausrechnen und kannst sie anschließend mit diesen vergleichen. <br /> | ||
'''a)''' Zu welcher Uhrzeit befinden sich am meisten Besucher in dem Zoo? Und wie viele sind es?<br/> | '''a)''' Zu welcher Uhrzeit befinden sich am meisten Besucher in dem Zoo? Und wie viele sind es?<br/> | ||
| − | <popup name="Tipp">Die Ableitung lautet: | + | <popup name="Tipp">Die Ableitung lautet: b´(t) = - 0,15 t² + 3,6 t - 19,2 </popup> |
| − | <popup name="Lösung">Die Nullstellen der Ableitung entsprechen den Maximalstellen der Normalfunktion. Setzt man die Ableitung gleich 0, also 0 = | + | <popup name="Lösung">Die Nullstellen der Ableitung entsprechen den Maximalstellen der Normalfunktion. Setzt man die Ableitung gleich 0, also 0 = b´(t) = - 0,15 t² + 3,6 t - 19,2 , dann erhält man t_1 = 8 und t_2 = 16. Da der Zoo erst um 10:00 Uhr (also t = 10) öffnet, ist t_2 die einzige Lösung. <br/> Setzt man das in die Funktion ein erhält man: b(16) = 11,3 . <br/>'''Die Antwort: Mit 1130 Besuchern sind um 16:00 Uhr die meisten Menschen im Zoo.</popup> |
<br/> | <br/> | ||
'''b)''' Wann ist die Besucherzahl am geringsten? Und warum ist es falsch, an dieser Stelle nach der Minimalstelle zu suchen? <br/> | '''b)''' Wann ist die Besucherzahl am geringsten? Und warum ist es falsch, an dieser Stelle nach der Minimalstelle zu suchen? <br/> | ||
| Zeile 13: | Zeile 19: | ||
'''c)''' Zu welcher Uhrzeit ist der Andrang in den Zoo am größten? <br/> | '''c)''' Zu welcher Uhrzeit ist der Andrang in den Zoo am größten? <br/> | ||
<popup name="Tipp 1">Mit der Frage nach dem größten Andrang ist der größte Zuwachs an Besuchern gemeint.</popup> | <popup name="Tipp 1">Mit der Frage nach dem größten Andrang ist der größte Zuwachs an Besuchern gemeint.</popup> | ||
| − | <popup name="Tipp 2">Die zweite Ableitung lautet: | + | <popup name="Tipp 2">Die zweite Ableitung lautet: b´´(t) = - 0,3 t + 3,6</popup> |
<popup name="Lösung">Indem die zweite Ableitung gleich 0 gesetzt wird, kann man die Wendestelle ausrechnen. Daraus ergibt sich t = 12. Also sind die meisten Menschen um 12:00 Uhr auf den Weg in den Zoo.</popup><br /> | <popup name="Lösung">Indem die zweite Ableitung gleich 0 gesetzt wird, kann man die Wendestelle ausrechnen. Daraus ergibt sich t = 12. Also sind die meisten Menschen um 12:00 Uhr auf den Weg in den Zoo.</popup><br /> | ||
<br /> }} | <br /> }} | ||
==Aufgabe 6: Die Autofahrt== | ==Aufgabe 6: Die Autofahrt== | ||
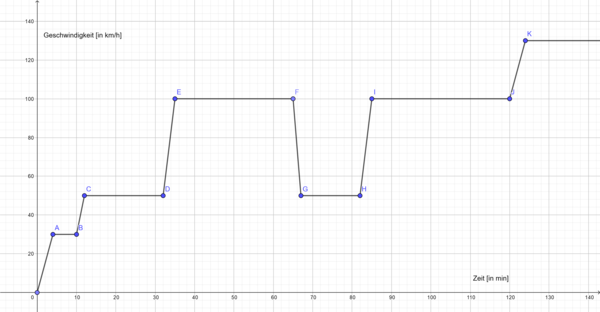
| − | {{Aufgaben| 6 | + | {{Aufgaben| 6 : Die Autofahrt|Familie Müller fährt zusammen in den Urlaub. Der Sohn Peter möchte gerne wissen, wie weit sie insgesamt gefahren sind. Dazu hat er die Geschwindigkeit des Autos zu bestimmten Zeitpunkten auf der Anzeige im Auto abgelesen und sich notiert. Die Geschwindigkeit könnte man in einem Graphen darstellen, wie in Abbildung 6.1. <br/> |
[[Datei:Geschwindigkeitsnotizen1.png|600px|zentriert|thumb|Geschwindigkeitsprofil einer Urlaubsfahrt]]<br /> | [[Datei:Geschwindigkeitsnotizen1.png|600px|zentriert|thumb|Geschwindigkeitsprofil einer Urlaubsfahrt]]<br /> | ||
Aktuelle Version vom 12. Januar 2019, 22:49 Uhr
Über mich
- Seminar: Wikiprojekt zu dem Seminar "DiWerS
- Projekt: Trainingsfeld Ableitungen
- betreut von: Elena Jedtke
Aufgabe 5: Ein Tag im Zoo
|
{{{2}}} |
Die Lösungen musst du per Hand ausrechnen und kannst sie anschließend mit diesen vergleichen.
a) Zu welcher Uhrzeit befinden sich am meisten Besucher in dem Zoo? Und wie viele sind es?
b) Wann ist die Besucherzahl am geringsten? Und warum ist es falsch, an dieser Stelle nach der Minimalstelle zu suchen?
c) Zu welcher Uhrzeit ist der Andrang in den Zoo am größten?
}}
Aufgabe 6: Die Autofahrt
|
Familie Müller fährt zusammen in den Urlaub. Der Sohn Peter möchte gerne wissen, wie weit sie insgesamt gefahren sind. Dazu hat er die Geschwindigkeit des Autos zu bestimmten Zeitpunkten auf der Anzeige im Auto abgelesen und sich notiert. Die Geschwindigkeit könnte man in einem Graphen darstellen, wie in Abbildung 6.1. a) Fülle die Lücken mit den richtigen Antworten.
c) Wie viele Kilometer ist das Auto von Peters Familie in dem Zeitraum von Minute 67 bis Minute 82 gefahren? Schreibe die Lösung in dein Heft. d) Wie viele Kilometer hat Peters Familie in den ersten 2 Stunden näherungsweise zurückgelegt? "Näherungsweise" bedeutet an dieser Stelle musst du nur die Phasen konstanter Geschwindigkeit in Betracht ziehen. Schreibe die Lösung in dein Heft.
Schreibe die Lösung in dein Heft. f) Berechne die durchschnittliche Geschwindigkeit, die Peters Familie in den ersten zwei Stunden gefahren ist. |