Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Wiederholung:Ganzrationale Funktionen: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 1: | Zeile 1: | ||
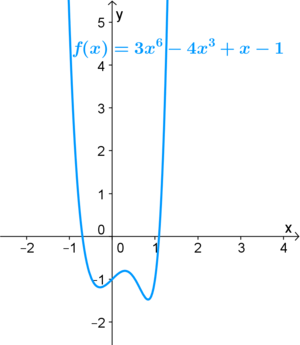
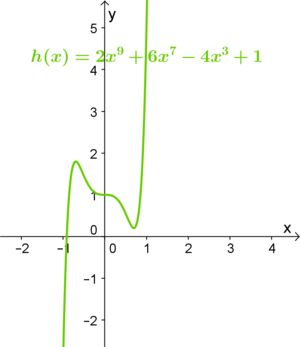
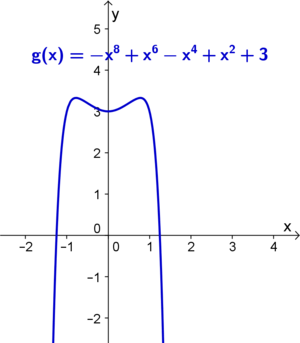
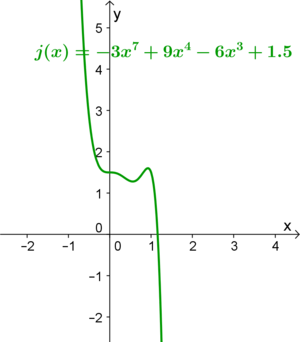
| − | Bei ganzrationalen Funktionen ist der '''Grad der Funktion''', sowie das '''Vorzeichen des Leitkoeffizienten''' ausschlaggebend, zu welchem der vier charakteristischen Verläufe die Funktion gehört:<br /> | + | Bei ganzrationalen Funktionen ist der '''Grad der Funktion''', sowie das '''Vorzeichen des Leitkoeffizienten''' dafür ausschlaggebend, zu welchem der vier charakteristischen Verläufe die Funktion gehört:<br /> |
{| | {| | ||
| Zeile 16: | Zeile 16: | ||
[[Datei:Oben-unten.png|300px]] | [[Datei:Oben-unten.png|300px]] | ||
|} | |} | ||
| + | |||
| + | <br /> | ||
| + | <br /> | ||
| + | Teste dein Wissen mit dieser Aufgabe aus dem Känguru-Wettbewerb 2013:<br /> | ||
| + | <br /> | ||
| + | <iframe src="http://LearningApps.org/watch?v=pfiz98zzc" style="border:0px;width:100%;height:1100px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | <br /> | ||
| + | |||
| + | <popup name="Lösung"> | ||
| + | Die Funktion hat eine einfache Nullstelle bei a (der Graph schneidet die x- Achse) und eine doppelte Nullstelle bei b (der Graph berührt die x- Achse).<br /> | ||
| + | -> mögliche Lösungen: A, B, C, D<br /> | ||
| + | <br /> | ||
| + | Da a < b ist, muss die einfache Nullstelle vor der doppelten liegen.<br /> | ||
| + | -> mögliche Lösungen: A, D<br /> | ||
| + | <br /> | ||
| + | Ausmultiplizieren des Funktionsterms ergibt W(x) = - x<sup>3</sup> +...<br /> | ||
| + | W(x) hat den Leitkoeffizienten: -1.<br /> | ||
| + | Damit verläuft die Funktion von links oben nach rechts unten.<br /> | ||
| + | -> Lösung: A | ||
| + | |||
| + | </popup> | ||
<br /> | <br /> | ||
Version vom 31. Mai 2013, 18:09 Uhr
Bei ganzrationalen Funktionen ist der Grad der Funktion, sowie das Vorzeichen des Leitkoeffizienten dafür ausschlaggebend, zu welchem der vier charakteristischen Verläufe die Funktion gehört:
| | ||
Teste dein Wissen mit dieser Aufgabe aus dem Känguru-Wettbewerb 2013:
| Zurück zu den Grenzwerten im Unendlichen |
Manipulationen an Funktionen