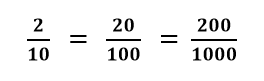Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Dezimalbrüche: Unterschied zwischen den Versionen
| Zeile 59: | Zeile 59: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Version vom 4. April 2018, 17:49 Uhr
In dem Nenner eines Dezimalbruchs steht eine natürliche Zahl der Zehnerpotenz.
Mit anderen Worten: Ein Bruch in dessen Nenner 10, 100, 1000, usw… steht. Deshalb wird der Dezimalbruch auch häufig als Zehnerbruch bezeichnet!
Hier ein Beispiel eines Dezimalbruchs:
In Dezimalschreibweise: 0,2 = 0,20 = 0,200
Wie zu erkennen ist kann man bei diesem Beispiel Arbeit ersparen und die Nullen am Ende weglassen, da sich die vorliegende Zahl dadurch nicht verändert.
Natürlich kommen nicht nur Zehnerbrüche in der Mathematik vor. Deshalb sollest du wissen wie man einen Bruch in einen Dezimalbruch umwandelt.
Prüfe dazu, ob du den vorliegenden Bruch auf eine Zehnerpotenz erweitern oder kürzen kannst.
Hier ein paar Beispiele:
=
= 0,2
=
= 0,25
=
=
= 0,75
Der Bruch 
kann beispielsweise nicht auf eine Zehnerpotenz erweitert werden:
≈ 0,33
Diese Dezimalbrüche solltest du dir sorgfältig einprägen, da sie häufig in Aufgaben verwendet werden!
= 0,5
= 0,125
= 0,1
= 0,0625
Hier geht's zum nächsten Kapitel!
| zu Brüche als Quotienten | zum Runden von Dezimalzahlen |
