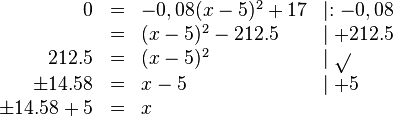Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Quadratische Funktionen: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 151: | Zeile 151: | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| + | {{Lösung versteckt mit Rand|1=<math> | ||
| + | \begin{array}{rll} | ||
| + | f(x)&=&x^2-8x+18 | ||
| + | \\ &=&x^2-8x+4^2-4^2+18 | ||
| + | \\ &=&(x-4)^2-16+18 | ||
| + | \\ &=&(x-4)^2+2 \\ | ||
| + | \end{array} | ||
| + | </math>}} | ||
<math> | <math> | ||
\begin{array}{rll} | \begin{array}{rll} | ||
Version vom 29. Mai 2018, 08:58 Uhr
|
In diesem Lernpfad geht es darum, dass du im Bereich der quadratischen Funktionen noch etwas sicherer wirst. Im Laufe dieses Lernpfads kannst du also noch einmal die Scheitelpunktform und die Normalform der quadratischen Funktion wiederholen und einige Übungsaufgaben dazu erledigen. Am Ende dieses Lernpfads erwartet dich dann noch eine Anwendungsaufgabe zu diesem Themengebiet. |
Inhaltsverzeichnis |
Die Scheitelpunktform
Die Parameter der Scheitelpunktform
|
Fülle den folgenden Lückentext aus.
|
Scheitelpunktformen und ihre Graphen
|
Ordne den angegebenen Graphen ihre Scheitelpunktform zu, indem du die zusammengehörigen Felder aufeinander ziehst. |
|
Skizziere die angegebenen Funktionen als Graphen auf ein Blatt Papier:
|
Funktionsgleichungen aufstellen
|
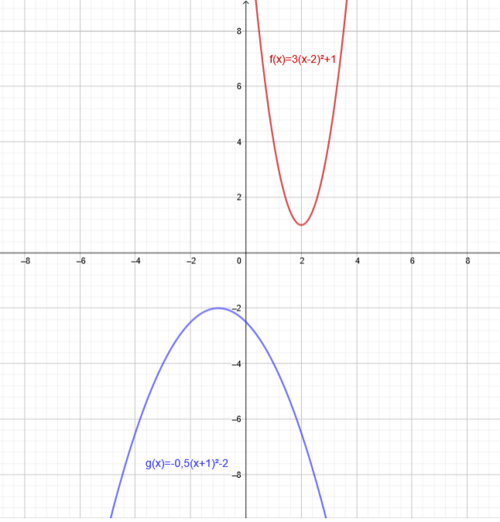
Stelle mit Hilfe der angegebenen Punkte die Funktionsgleichung auf: a) Wir suchen die Parabel f mit dem Scheitelpunkt S(-3I1), die durch den Punkt P(2I6) verläuft. b) Gesucht ist die Parabel g, die die y-Achse bei -4 schneidet, und die ihren Scheitelpunkt bei S(1I-1) hat. |
Scheitelpunktform und Normalform
|
Überlege dir noch einmal, wie die Scheitelpunktform in die Normalform und die Normalform in die Scheitelpunktform umgerechnet wird. |
Von der Scheitelpunktform zur Normalform
|
Forme die folgenden Scheitelpunktformen in deinem Heft in die Normalenformen um und klicke dann das richtige Ergebnis an. |
Von der Normalform zur Scheitelpunktform
In Aufgabe 5 hast du wiederholt, wie man die Normalform in die Scheitelpunktform überführt. Das kannst du in Aufgabe 9 üben. Zuerst wollen wir uns aber noch einmal genau ansehen, was die quadratische Ergänzung ist und warum man sie für die Umwandlung braucht. Wenn du dich mit der quadratischen Ergänzung schon sicher fühlst, kannst du direkt Aufgabe 9 bearbeiten.
Die quadratische Ergänzung ist ein Trick, den man benutzt, wenn die man die 1. oder 2. binomische Formel rückwärts anwenden anwenden möchte.
Zur Erinnerung:
30px Merke
1. Binomische Formel:
|
Wir wollen jetzt also nicht die Klammer ausmultiplizieren, sondern den Term zu so einem Klammerausdruck umformen, z.B. den Term 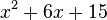 .
.
Wie das funktioniert, kannst du in dieser Aufgabe noch mal wiederholen:
|
|
Wichtig: Wenn for dem x2 ein Faktor steht, muss dieser zunächst ausgeklammert werden:
|
Ergänze in dem folgenden Beispiel die Umformungsschritte, indem du sie an die richtige Stelle ziehst. |
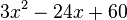 | Faktor 3 ausklammern
| Faktor 3 ausklammern
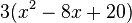 | Faktor 2 "herausziehen"
| Faktor 2 "herausziehen"
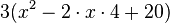 | quadratische Ergänzung
| quadratische Ergänzung
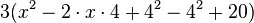 | 2. Binomische Formel
| 2. Binomische Formel
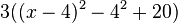 | zusammenfassen
| zusammenfassen
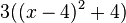 | ausmultiplizieren
| ausmultiplizieren
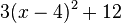
|
|
Anwendungsaufgabe "Turm"
|
Von einem Turm aus wird ein Stein geworfen. Die Wurfbahn ist parabelförmig und kann mit der Gleichung |
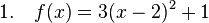
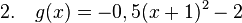

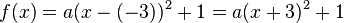
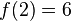
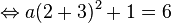
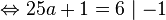
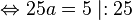
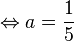
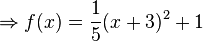
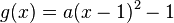
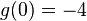
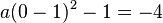
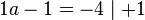
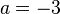
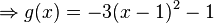
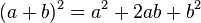
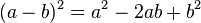
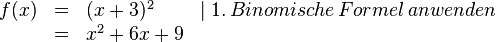
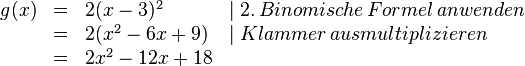
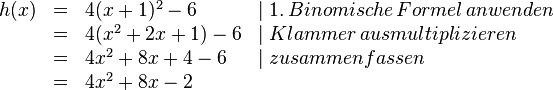
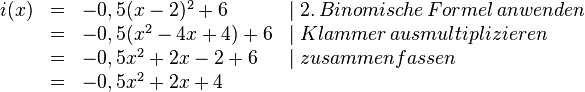
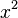 zunächst auszuklammern!
zunächst auszuklammern!
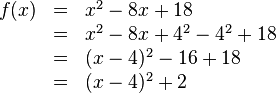
![\begin{array}{rll}
g(x)&=&5x^2+30x+43 \\ &=&5(x^2+6x+8.6) \\ &=&5(x^2+6x+3^2-3^2+8.6) \\ &=&5[(x+3)^2-3^2+8.6] \\ &=&5[(x+3)^2-0.4] \\ &=&5(x+3)^2-2
\end{array}](/images/math/f/4/c/f4c416dfb6dcdbadc261c78110aa4cf8.png)
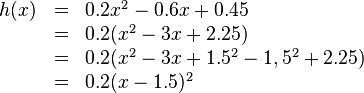
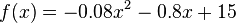
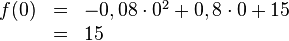
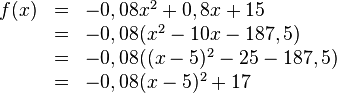
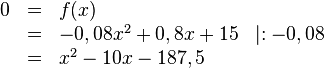
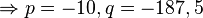
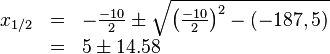
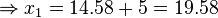 und
und