Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Unser Regelheft: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 7: | Zeile 7: | ||
=== '''Anordnung der rationalen Zahlen'''=== | === '''Anordnung der rationalen Zahlen'''=== | ||
Liegt auf der Zahlengeraden <math>a</math> links von <math>b</math>, so ist <math>a<b</math> | Liegt auf der Zahlengeraden <math>a</math> links von <math>b</math>, so ist <math>a<b</math> | ||
| + | [[Datei:Zahlenstrahl Anordnung.jpg|miniatur]] | ||
| + | ==='''Betrag'''=== | ||
| + | Der Abstand einer rationalen Zahl <math>a</math> von der Zahl 0 heißt der '''Betrag''' von <math>a</math>. Für den Betrag von <math>a</math> schreibt man <math>|a|</math>. (lies: Betrag von a) | ||
| + | <math>|+3|=|3|=3</math>; <math>|0|=0</math>; <math>|-5,6|=5,6</math> | ||
=== '''Rechengesetze für rationale Zahlen''' === | === '''Rechengesetze für rationale Zahlen''' === | ||
Version vom 8. September 2018, 14:47 Uhr
In diesem Bereich werden die Schüler*innen der Klasse 7d fortlaufend während des Schuljahres die Regeln, die im Unterricht entwickelt wurden, verschriftlichen.
Inhaltsverzeichnis |
Rechnen mit rationalen Zahlen
Anordnung der rationalen Zahlen
Liegt auf der Zahlengeraden 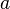 links von
links von 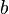 , so ist
, so ist 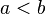
Betrag
Der Abstand einer rationalen Zahl  von der Zahl 0 heißt der Betrag von
von der Zahl 0 heißt der Betrag von 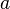 . Für den Betrag von
. Für den Betrag von 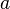 schreibt man
schreibt man  . (lies: Betrag von a)
. (lies: Betrag von a)
;
;
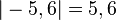
Rechengesetze für rationale Zahlen
a) Kommutativgesetz der Addition bzw. Multiplikation
Beim Addieren darf man die Summanden bzw. beim Multiplizieren darf man die Faktoren vertauschen z.B.:bzw.
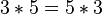
b) Assoziativgesetz der Addition bzw. der Multiplikation
Addiert bzw. multipliziert man mehrere Zahlen, so darf man Klammern beliebig umsetzen oder weglassen z.B.:bzw.
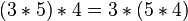
c) Distributivgesetz der Multiplikation
Statt eine Zahl mit einer Summe zu multiplizieren, kann man auch zuerst die Zahl mit jedem Summanden multiplizieren. z.B.:Ähnliches gilt bei einer Differenz
d) Distributivgesetz der Division
Statt eine Summe durch eine Zahl zu dividieren, kann man auch zuerst jeden Summanden durch die Zahl dividieren. z.B.:Ähnliches gilt bei einer Differenz

