Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Benutzer:Julia WWU3: Unterschied zwischen den Versionen
(→Zusammenhang von durchschnittlicher und momentaner Änderungsrate) |
(→Zusammenhang von durchschnittlicher und momentaner Änderungsrate) |
||
| Zeile 37: | Zeile 37: | ||
<iframe src="https://learningapps.org/watch?v=pdbfw1aq318" style="border:0px;width:100%;height:300px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=pdbfw1aq318" style="border:0px;width:100%;height:300px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| − | <popup name="Tipp zu 3a. | + | <popup name="Tipp zu 3a.3) zum Lückentext">Der Grenzwert des Differenzenquotienten ist der Differentialquotient <math> \lim_{x \to 2} \frac{f(2)-f(x)} {2-x}</math></popup> |
<popup name="Lösung zu 1)">Je näher man den x-Wert an 2 annähert, desto kleiner wird der Wert des Differenzenquotienten. Er nähert sich von anfänglich -0,95 immer näher an -1 an. So liegt der Wert des Differenzenquotienten bei 1,99 bei -0,995.</popup> | <popup name="Lösung zu 1)">Je näher man den x-Wert an 2 annähert, desto kleiner wird der Wert des Differenzenquotienten. Er nähert sich von anfänglich -0,95 immer näher an -1 an. So liegt der Wert des Differenzenquotienten bei 1,99 bei -0,995.</popup> | ||
Version vom 14. November 2018, 11:13 Uhr
Zusammenhang von durchschnittlicher und momentaner Änderungsrate
 Aufgabe 3: Zusammenhang von mittleren und lokalen Änderungsrate
a) Diese Funktion ist in der folgenden Abbildung dargestellt:
In der folgenden Tabelle siehst du einige Funktionswerte aufgelistet. Außerdem wurden die Differenzenquotienten vom Punkt 
1) Beschreibe, was mit dem Differenzenquotient passiert, wenn sich die x-Werte 2 annähern. 2) Erkläre, warum in der letzten Zeile unter "Differenzenquotient" ein "?" eingetragen ist. 3) Was bedeutet das Ergebnis aus 1) für die durchschnittliche Änderungsrate und was bedeutet es für die momentane Änderungsrate im Punkt (2 ; 2,5)? Wie hängen diese beiden Begriffe miteinander zusammen? Beantworte diese Fragen selbst oder löse dazu den Lückentext.
b) (Forder-Aufgabe) Sieh dir zunächst die Formeln und die Abbildung in der Darstellung an. Durch Verschieben des Δx-Knopfs verändern sich die Werte in den Formeln und die Abbildung. Probier einmal aus, was sich verändert.
1) Was gibt die Variable ks an? 2) Fülle nun den folgenden Lückentext aus.
|
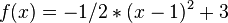
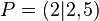mit Punkten in der Umgebung ausgerechnet.
