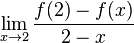Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Von der mittleren zur lokalen Änderungsrate: Unterschied zwischen den Versionen
| Zeile 175: | Zeile 175: | ||
==Zusammenhang von durchschnittlicher und momentaner Änderungsrate== | ==Zusammenhang von durchschnittlicher und momentaner Änderungsrate== | ||
| − | {{Aufgaben|5: Zusammenhang von | + | {{Aufgaben|5: Zusammenhang von mittleren und lokalen Änderungsrate| <math>f(x) = -1/2*(x-1)^2+3</math> |
Diese Funktion ist in der folgenden Abbildung dargestellt: | Diese Funktion ist in der folgenden Abbildung dargestellt: | ||
| Zeile 181: | Zeile 181: | ||
<iframe scrolling="no" title="Graph der Funktion" src="https://www.geogebra.org/material/iframe/id/kpxhhjdq/width/800/height/482/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="1000px" height="482px" style="border:0px;"> </iframe> | <iframe scrolling="no" title="Graph der Funktion" src="https://www.geogebra.org/material/iframe/id/kpxhhjdq/width/800/height/482/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="1000px" height="482px" style="border:0px;"> </iframe> | ||
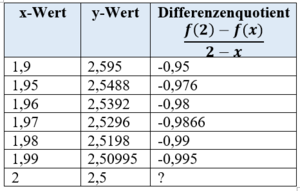
| − | In der folgenden Tabelle siehst du einige Funktionswerte aufgelistet. Außerdem wurden die Differenzenquotienten vom Punkt (2 | + | In der folgenden Tabelle siehst du einige Funktionswerte aufgelistet, die du auch in der obigen Graphik ablesen kannst. Außerdem wurden die Differenzenquotienten vom Punkt <math>P = (2|2,5)</math> mit Punkten in der Umgebung ausgerechnet. |
| − | [[Datei:Tabelle | + | [[Datei:Tabelle Grenzwert.PNG|300px|links|rahmenlos|Tabelle zu x-, y-Werten und dem Differenzenquotienten zu der gegebenen Funktion f]] |
| Zeile 207: | Zeile 207: | ||
<popup name="Tipp zu 3a.2)">Überlege, welche Werte im Zähler und im Nenner des Differenzenquotienten in dieser Zeile stünden.</popup> | <popup name="Tipp zu 3a.2)">Überlege, welche Werte im Zähler und im Nenner des Differenzenquotienten in dieser Zeile stünden.</popup> | ||
| − | '''c)''' Was bedeutet das Ergebnis aus 1) für die durchschnittliche Änderungsrate und was bedeutet es für die momentane Änderungsrate im Punkt (2 ; 2,5)? Wie hängen diese beiden Begriffe miteinander zusammen? Beantworte diese Fragen selbst oder löse dazu den Lückentext. | + | '''c)''' Was bedeutet das Ergebnis aus 1) für die durchschnittliche Änderungsrate und was bedeutet es für die momentane Änderungsrate im Punkt (2 ; 2,5)? Wie hängen diese beiden Begriffe miteinander zusammen? Beantworte diese Fragen selbst oder löse dazu den Lückentext. Dabei beziehen sich die Lücken immer auf <math>\frac {f(2)-f(x)} {2-x}</math>. |
<iframe src="https://learningapps.org/watch?v=pdbfw1aq318" style="border:0px;width:100%;height:300px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=pdbfw1aq318" style="border:0px;width:100%;height:300px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| − | <popup name="Tipp zu 3a. | + | <popup name="Tipp zu 3a.3) zum Lückentext">Der Grenzwert des Differenzenquotienten ist der Differentialquotient <math> \lim_{x \to 2} \frac{f(2)-f(x)} {2-x}</math></popup> |
<popup name="Lösung zu 1)">Je näher man den x-Wert an 2 annähert, desto kleiner wird der Wert des Differenzenquotienten. Er nähert sich von anfänglich -0,95 immer näher an -1 an. So liegt der Wert des Differenzenquotienten bei 1,99 bei -0,995.</popup> | <popup name="Lösung zu 1)">Je näher man den x-Wert an 2 annähert, desto kleiner wird der Wert des Differenzenquotienten. Er nähert sich von anfänglich -0,95 immer näher an -1 an. So liegt der Wert des Differenzenquotienten bei 1,99 bei -0,995.</popup> | ||
| Zeile 217: | Zeile 217: | ||
<popup name="Lösung zu 2)">In dieser Zeile müsste man 0/0 rechnen. Dies ist keine zulässige Rechenoperation, also nicht berechenbar.</popup> | <popup name="Lösung zu 2)">In dieser Zeile müsste man 0/0 rechnen. Dies ist keine zulässige Rechenoperation, also nicht berechenbar.</popup> | ||
| − | <popup name="Lösung zu 3)"> Wenn der Differenzenquotient einen bestimmten Wert, z.B. 0,95 bei x=1,9, annimmt, entspricht | + | <popup name="Lösung zu 3)"> Wenn der Differenzenquotient einen bestimmten Wert, z.B. -0,95 bei x=1,9, annimmt, entspricht der der mittleren Änderungsrate der Funktion im Intervall [1,9;2]. Wenn man kleinere Intervalle betrachtet, nähert sich der Differenzenquotient -1 an. Das bedeutet, in der Umgebung von x=2 liegt die Änderungsrate nahe bei -1. Da die Änderungsrate in einem Punkt von dem Differentialquotient angegeben wird, entspricht der der Grenzwert des Differenzenquotienten <math> \lim_{x \to 2} \frac{f(2)-f(x)} {2-x}</math> dem Differentialquotienten. Letzterer gibt die momentane Änderungsrate im Punkt x=2 an.</popup>}} |
| − | {{Aufgaben|6: graphischer Zusammenhang von | + | {{Aufgaben|6: graphischer Zusammenhang von mittleren und lokalen Änderungsrate|(Forder-Aufgabe) |
Sieh dir zunächst die Formeln und die Abbildung in der Darstellung an. Durch Verschieben des Δx-Knopfs verändern sich die Werte in den Formeln und die Abbildung. Probier einmal aus, was sich verändert. | Sieh dir zunächst die Formeln und die Abbildung in der Darstellung an. Durch Verschieben des Δx-Knopfs verändern sich die Werte in den Formeln und die Abbildung. Probier einmal aus, was sich verändert. | ||
| Zeile 248: | Zeile 248: | ||
4)sinkt | 4)sinkt | ||
| − | 5)die Steigung der Funktion im Punkt | + | 5)die Steigung der Funktion im Punkt <math>x_0</math> |
6)dem Differentialquotienten | 6)dem Differentialquotienten | ||
7)0,8</popup>}} | 7)0,8</popup>}} | ||
Version vom 16. November 2018, 12:12 Uhr
|
Dieser Lernpfad beschäftigt sich mit der mittleren und lokalen Änderungsrate. In Aufgabe 1 geht es darum, die mittlere Änderungsrate zu berechnen. Dies erfolgt in Teilaufgabe a) anhand von Rechenbeispielen. In b) hingegen übst du mittlere Änderungsraten im Sachzusammenhang zu berechnen. Dies ist eine Förderaufgabe. Wenn du schon sicher im Umgang mit mittleren Änderungsraten bist, kannst du diese Aufgabe auch überspringen. In Aufgabe 2 beschäftigst du dich mit der Unterscheidung der mittleren und lokale Änderungsrate. In Teilaufgaben a) und b) geht es darum, festzustellen, wie sich die beiden Änderungsraten unterscheiden. In Teilaufgabe c) musst du im Sachzusammenhang unterscheiden, welche der beiden Änderungsraten berechnet werden soll. Diese Aufgabe ist eine Förderaufgabe. Den Zusammenhang von mittlerer und lokaler Änderungsrate erarbeitest du in Aufgabe 3. Teilaufgabe a) ist eine Förderaufgabe. In Teilaufgabe b) geht es um die graphischen Zusammenhänge. Dies ist eine Forderaufgabe. |
Inhaltsverzeichnis |
Bestimmung von mittleren Änderungsraten
|
Berechne die mittlere Änderungsrate in den angegebenen Intervallen zunächst auf einem separaten Blatt Papier. Prüfe im Anschluss die von dir errechneten Werte, indem du sie in die dafür vorgesehenen Kästchen unter der Aufgabe eingibst.
|
|
Leider ist der Vorstand wegen der Vorbereitung der Jubiläumsfeier sehr beschäftigt und bittet dich, ihm bei der Beantwortung einiger Fragen zu helfen. a) Wie viele Mitglieder sind seit 2010 im Durchschnitt pro Jahr in deinem Verein hinzugekommen? |
(!30) (!2,4) (!24) (!29,71) (26)
b) Der aktuelle Vorstand arbeitet seit 2016 zusammen. Sein Ziel war eine Steigerung der Mitgliedszahlen. Diese sollte im Mittel größer sein als der durchschnittliche Mitgliederzuwachs in den Jahren davor (also von Beginn der Mitgliedererfassung bis zur Wahl des neuen Vorstands 2016). Ist es Ihnen gelungen ihr Ziel zu erreichen?
(Ja, es ist Ihnen gelungen ihr Ziel zu erreichen.) (!Nein, sie haben ihr Ziel nicht erreicht.) (!Sowohl vor der Wahl als auch nach der Wahl des neuen Vorstands sind im Durchschnitt pro Jahr genau gleich viele Mitglieder dem Verein beigetreten.)
Unterscheidung der Änderungsraten
|
a) Unterscheidung der mittleren und lokalen Änderungsrate Ordne die verschiedenen Begriffe der richtigen Änderungsrate zu.
Fertige in deinem Heft eine Tabelle zur durchschnittlichen und momentanen Änderungsrate mit den Begriffen aus Teilaufgabe a an. Stelle die zueinander passenden Begriffe gegenüber. |
|
Tim fährt mit dem Fahrrad zur Schule und muss an einer roten Ampel abbremsen. Für den in der Zeit t (in Sekunden) zurückgelegten Weg s(t) (in Meter) gilt:
a) Berechne den zurückgelegten Weg nach 3 und 5 Sekunden. b) Berechne die Geschwindigkeit, die Tim nach 3 Sekunden bzw. nach 5 Sekunden mit seinem Fahrrad erreicht hat. c) Warum hat die oben genannte Formel im vorliegenden Sachzusammenhang für
|
Zusammenhang von durchschnittlicher und momentaner Änderungsrate
|
Diese Funktion ist in der folgenden Abbildung dargestellt:
In der folgenden Tabelle siehst du einige Funktionswerte aufgelistet, die du auch in der obigen Graphik ablesen kannst. Außerdem wurden die Differenzenquotienten vom Punkt
a) Beschreibe, was mit dem Differenzenquotient passiert, wenn sich die x-Werte 2 annähern. b) Erkläre, warum in der letzten Zeile unter "Differenzenquotient" ein "?" eingetragen ist. c) Was bedeutet das Ergebnis aus 1) für die durchschnittliche Änderungsrate und was bedeutet es für die momentane Änderungsrate im Punkt (2 ; 2,5)? Wie hängen diese beiden Begriffe miteinander zusammen? Beantworte diese Fragen selbst oder löse dazu den Lückentext. Dabei beziehen sich die Lücken immer auf
|
|
(Forder-Aufgabe) Sieh dir zunächst die Formeln und die Abbildung in der Darstellung an. Durch Verschieben des Δx-Knopfs verändern sich die Werte in den Formeln und die Abbildung. Probier einmal aus, was sich verändert.
a) Was gibt die Variable ks an? b) Fülle nun den folgenden Lückentext aus.
|
 im Intervall
im Intervall ![[2,5]](/images/math/d/b/5/db5dc72ec1da78e609bf9f0ae1447688.png)
 im Intervall
im Intervall ![[2,7]](/images/math/1/1/f/11fa16d050ab48b2dd318ff5b5817119.png)
 im Intervall
im Intervall ![[-2,1]](/images/math/7/0/1/7019f6fe0e7078b019e0586e7cbc564a.png)
 .
. und
und 
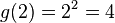 und
und 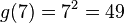
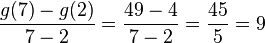
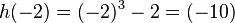 und
und 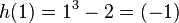
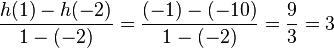

![[2010, 2018]](/images/math/2/8/e/28e3440d83b68a73b89015a371d2b0f6.png) gesucht. Wenn du nicht mehr weißt, wie du diese berechnen kannst, lies in den Tipps zu Aufgabe 1 nach.
gesucht. Wenn du nicht mehr weißt, wie du diese berechnen kannst, lies in den Tipps zu Aufgabe 1 nach. 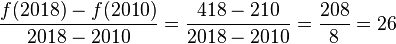
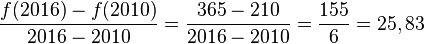
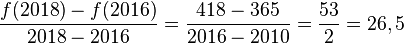
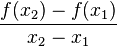 stellt den Differenzenquotienten dar. Der Differenzenquotient gibt die durchschnittliche Änderungsrate von f über dem Intervall [
stellt den Differenzenquotienten dar. Der Differenzenquotient gibt die durchschnittliche Änderungsrate von f über dem Intervall [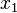 ;
;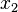 ] an.
] an.
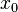 |
|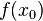 ) und Q(
) und Q(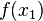 ).
).
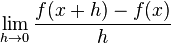 heißt Differentialquotient. Dieser Quotient ist der Grenzwert des Differenzenquotienten. Er gibt die Steigung der Tangente an der Stelle x an und entspricht der Ableitung an dieser Stelle.
heißt Differentialquotient. Dieser Quotient ist der Grenzwert des Differenzenquotienten. Er gibt die Steigung der Tangente an der Stelle x an und entspricht der Ableitung an dieser Stelle.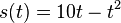 für
für ![t\in [0;5]](/images/math/d/1/7/d17e4f93b0be76b84d0dd79694840cff.png)
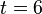 keinen Sinn?
keinen Sinn?
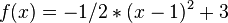
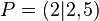 mit Punkten in der Umgebung ausgerechnet.
mit Punkten in der Umgebung ausgerechnet.
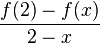 .
.