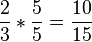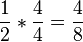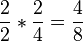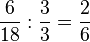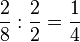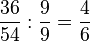Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Erweitern und Kürzen: Unterschied zwischen den Versionen
| Zeile 6: | Zeile 6: | ||
Als '''Bruchrechnung''' bezeichnet man das Rechnen mit ''gemeinen Brüchen'' in der „Zähler-Bruchstrich-Nenner-Schreibweise“. | Als '''Bruchrechnung''' bezeichnet man das Rechnen mit ''gemeinen Brüchen'' in der „Zähler-Bruchstrich-Nenner-Schreibweise“. | ||
| − | Die Regeln der Bruchrechnung beziehen sich auf die '''Grundrechenarten''', also auf Addition, Subtraktion, Multiplikation, Division und Kehrwertbildung. Außerdem gibt eine '''Kürzungs- und Erweiterungsregel''', zu der es weiter unten auch ein eigenes Thema gibt. | + | Die Regeln der Bruchrechnung beziehen sich auf die '''Grundrechenarten''', also auf Addition, Subtraktion, Multiplikation, Division und Kehrwertbildung. |
| + | |||
| + | Außerdem gibt eine '''Kürzungs- und Erweiterungsregel''', zu der es weiter unten auch ein eigenes Thema gibt. | ||
Version vom 8. Februar 2018, 14:10 Uhr
Was ist überhaupt ein Bruch?
Als Bruchrechnung bezeichnet man das Rechnen mit gemeinen Brüchen in der „Zähler-Bruchstrich-Nenner-Schreibweise“.
Die Regeln der Bruchrechnung beziehen sich auf die Grundrechenarten, also auf Addition, Subtraktion, Multiplikation, Division und Kehrwertbildung.
Außerdem gibt eine Kürzungs- und Erweiterungsregel, zu der es weiter unten auch ein eigenes Thema gibt.
Nun zum ersten Thema des Lernpfades.
-> Erweitern und Kürzen:
Erweitern: Multipliziere Zähler und Nenner des Bruches mit derselben natürlichen Zahl, welche nicht 0 sein darf!
Kürzen: Dividiere Zähler und Nenner des Bruches durch dieselbe natürliche Zahl!
Nun gibt es hier ein kleines Beispiel, mit dem ihr testen könnt, ob ihr die Grundregeln verstanden habt. Viel Spaß!
Zuordnungs-Quiz
|