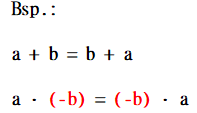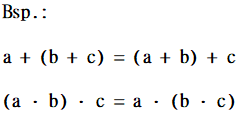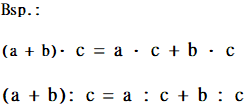Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Rechenvorteile: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 57: | Zeile 57: | ||
Aufgabe 1 | Aufgabe 1 | ||
<iframe src="https://learningapps.org/watch?v=p7pp4vtnv18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=p7pp4vtnv18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | </popup> | ||
| + | |||
| + | |||
| + | {{Vorlage:Lesepfad Ende | ||
| + | |Link zurück=[[Julius-Echter-Gymnasium/Mathematik/Rechnen mit rationalen Zahlen|zu Rechnen mit rationalen Zahlen]] | ||
| + | |Link vor=[[Julius-Echter-Gymnasium/Mathmatik/Berechnung von Grundwert, Prozentsatz und Prozentwert|zu Berechnung von Grundwert, Prozentsatz und Prozentwert]] | ||
| + | |Text Copyright= | ||
| + | }} | ||
Version vom 31. März 2018, 12:58 Uhr
Rechenvorteile
Die bereits bekannten Rechenvorteile gelten ebenso bei den rationalen Zahlen ebenso:
1) Kommutativgesetz
Beachte: Du musst die Vorzeichen der Zahlen immer mitnehmen!
2) Assoziativgesetz
Beachte: Die Klammern musst du immer zuerst berechnen!
3) Distributivgesetz
Beachte: Punkt vor Strich!
Verbindung der Grundrechenarten
Hier hast du ein vorgerechnetes Beispiel anhand dieses Terms:
(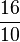 + 4,5) :
+ 4,5) :  + (2ˑ10-2,25)
+ (2ˑ10-2,25)
Schritt 1: 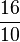 + 4,5 =
+ 4,5 = 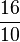 +
+  =
= 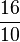 +
+ 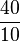 =
= 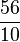 = 5,6
= 5,6
Schritt 2:  = 0,4
= 0,4
Schritt 3: (2ˑ10-2,25) = (20-2,25) = 17,75
Schritt 4: (5,6 : 0,4) + 17,75 = 33
| zu Rechnen mit rationalen Zahlen | zu Berechnung von Grundwert, Prozentsatz und Prozentwert |