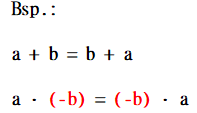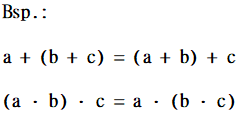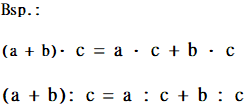Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Rechenvorteile: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 49: | Zeile 49: | ||
| − | '''''<span style="color: #FF0000">Schritt 3:</span>''''' <big> ( | + | '''''<span style="color: #FF0000">Schritt 3:</span>''''' <big> (2·10−2,25)</big> = <big>(20−2,25)</big> = <big> 17,75</big> |
Version vom 31. März 2018, 13:06 Uhr
Rechenvorteile
Die bereits bekannten Rechenvorteile gelten ebenso bei den rationalen Zahlen ebenso:
1) Kommutativgesetz
Beachte: Du musst die Vorzeichen der Zahlen immer mitnehmen!
2) Assoziativgesetz
Beachte: Die Klammern musst du immer zuerst berechnen!
3) Distributivgesetz
Beachte: Punkt vor Strich!
Verbindung der Grundrechenarten
Hier hast du ein vorgerechnetes Beispiel anhand dieses Terms:
(
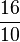+ 4,5) : 
+ (2·10−2,25)
Schritt 1: 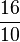+ 4,5 = + 
= + 
= 
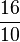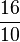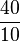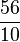= 5,6
Schritt 2: = 0,4
Schritt 3: (2·10−2,25) = (20−2,25) = 17,75
Schritt 4: (5,6 : 0,4) + 17,75 = 33
| zu Rechnen mit rationalen Zahlen | zu Berechnung von Grundwert, Prozentsatz und Prozentwert |
