Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Test: Unterschied zwischen den Versionen
(Arbeiten -> Aufgaben) |
|||
| Zeile 2: | Zeile 2: | ||
== <span style="color:blue"> '''Teil Sophia:''' </span><br /><br />== | == <span style="color:blue"> '''Teil Sophia:''' </span><br /><br />== | ||
| − | {{ | + | {{Aufgaben|1=1a|2= Ein Werfer wirft einen Ball. Die Flugkurve des Balls kann näherungsweise durch die Funktion <math>f(x)=-0,02x^2+1,2x+2,08</math> beschrieben werden. Den Flug des Balls können Sie unter folgendem Link genauer betrachten. Lassen Sie hierzu den roten Ball fliegen, indem Sie bei dem roten Ball auf play drücken. Die anderen Punkte sollten sie nicht bewegen! }} |
https://ggbm.at/J94wAFh3 | https://ggbm.at/J94wAFh3 | ||
| − | {{ | + | {{Aufgaben|1=1b|2= Bestimmen Sie die Steigung des Balls an den verschiedenen Punkten der Flugkurve. }} |
<iframe src="https://learningapps.org/watch?v=pvda4vyqn17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> <br /> | <iframe src="https://learningapps.org/watch?v=pvda4vyqn17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> <br /> | ||
| − | {{ | + | {{Aufgaben|1=1c|2= Ordnen Sie die Begriffe und Interpretationen den Markierungen auf dem Graphen zu. Hierzu müssen Sie die verschiedenen Markierungen anklicken und anschließend eine der vorgeschlagenen Möglichkeiten auswählen. }} |
<iframe src="https://learningapps.org/watch?v=p2nv88km317" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=p2nv88km317" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
<br /> | <br /> | ||
| − | {{ | + | {{Aufgaben|1=1d|2=Füllen Sie die Lücken, indem Sie die Aufgabe im Sachzusammenhang interpretieren. }} |
<iframe src="https://learningapps.org/watch?v=pt8k3bz3c17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=pt8k3bz3c17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
Aktuelle Version vom 29. April 2018, 10:43 Uhr
Teil Sophia:
|
Ein Werfer wirft einen Ball. Die Flugkurve des Balls kann näherungsweise durch die Funktion |
|
Bestimmen Sie die Steigung des Balls an den verschiedenen Punkten der Flugkurve. |
|
Ordnen Sie die Begriffe und Interpretationen den Markierungen auf dem Graphen zu. Hierzu müssen Sie die verschiedenen Markierungen anklicken und anschließend eine der vorgeschlagenen Möglichkeiten auswählen. |
|
Füllen Sie die Lücken, indem Sie die Aufgabe im Sachzusammenhang interpretieren. |
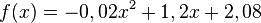 beschrieben werden. Den Flug des Balls können Sie unter folgendem Link genauer betrachten. Lassen Sie hierzu den roten Ball fliegen, indem Sie bei dem roten Ball auf play drücken. Die anderen Punkte sollten sie nicht bewegen!
beschrieben werden. Den Flug des Balls können Sie unter folgendem Link genauer betrachten. Lassen Sie hierzu den roten Ball fliegen, indem Sie bei dem roten Ball auf play drücken. Die anderen Punkte sollten sie nicht bewegen!

