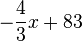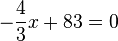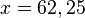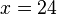Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Lineare Funktionen: Unterschied zwischen den Versionen
(→Schnittpunkt zweier Geraden) |
K (Größe des Applets bei Aufg. 3 angepasst) |
||
| Zeile 29: | Zeile 29: | ||
==Wertetabellen und lineare Funktionen== | ==Wertetabellen und lineare Funktionen== | ||
{{Aufgaben|3|Bestimme anhand der Tabellen die zugehörigen Funktionsgleichungen und tippe sie in die grauen Felder ein. | {{Aufgaben|3|Bestimme anhand der Tabellen die zugehörigen Funktionsgleichungen und tippe sie in die grauen Felder ein. | ||
| − | <iframe src="https://learningapps.org/watch?v=p3p1uf86j18" style="border:0px;width:100%;height: | + | <iframe src="https://learningapps.org/watch?v=p3p1uf86j18" style="border:0px;width:100%;height:250px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
<popup Name="Tipp 1">Lies den y-Achsenabschnitt an der Stelle x=0 ab.</popup> | <popup Name="Tipp 1">Lies den y-Achsenabschnitt an der Stelle x=0 ab.</popup> | ||
<popup Name="Tipp 2">Die Steigung m gibt an, wie weit sich die Funktion in y-Richtung verändert, wenn der x-Wert um eine Einheit steigt.</popup> | <popup Name="Tipp 2">Die Steigung m gibt an, wie weit sich die Funktion in y-Richtung verändert, wenn der x-Wert um eine Einheit steigt.</popup> | ||
Version vom 8. Juni 2018, 11:29 Uhr
|
In diesem Lernpfad kannst du dein Wissen über lineare Funktionen vertiefen und dieses anwenden. In Aufgabe 1-5 wiederholst du dabei noch einmal, wie lineare Funktionsgleichungen aufgestellt werden und wie man einen Graphen skizziert. Außerdem kannst du dich in Aufgabe 3 noch einmal mit Wertetabellen zu linearen Zuordnungen beschäftigen. Die Aufgaben 6 und 7 bieten dir die Möglichkeit, das Gelernte im Sachkontext anzuwenden. |
Inhaltsverzeichnis |
Lineare Funktionen im Überblick
|
Fülle folgenden Lückentext aus, indem du auf die leeren Felder klickst und die richtige Antwort auswählst |
Vom Graphen zur Funktionsgleichung
|
Ordne den folgenden Graphen die entsprechenden Funktionsgleichungen zu, indem du die zusammengehörigen Felder aufeinander legst. |
Wertetabellen und lineare Funktionen
|
Bestimme anhand der Tabellen die zugehörigen Funktionsgleichungen und tippe sie in die grauen Felder ein. |
Schnittpunkt zweier Geraden
|
Bestimme die Schnittpunkte von zwei Geraden zuerst zeichnerisch und dann rechnerisch in deinem Heft. a) b) |
Funktionsgleichung aufstellen anhand zweier vorgegebener Punkte
|
Bestimme rechnerisch die Funktionsgleichungen der linearen Funktion, die jeweils durch die angegebenen Punkte verläuft. Berechne jeweils die Nullstellen dieser Funktionen und bestimme, für welchen x-Wert die Funktionen jeweils den Wert 12 annehmen. Notiere deine Rechnung und Antwort in deinem Heft. a) b) c) |
Textaufgaben
|
Eine 15cm lange Kerze braucht 10 Stunden, um vollständig abzubrennen. Eine weitere und dünnere Kerze ist 20cm lang und brennt in nur 8 Stunden vollständig ab. a) Stelle für jede Kerze eine Funktionsgleichung auf und zeichne einen Graphen. b) Die Kerzen werden gleichzeitig angezündet. Nach wie viele Stunden sind die Kerzen gleich hoch? c)Welche Höhe haben die Kerzen nach 3 Stunden?
|
|
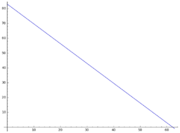
Aus einer zylinderförmigen Regentonne wird das Wasser gleichmäßig abgelassen. Nach 6 Minuten beträgt die Wasserhöhe noch 75cm, nach weiteren 15 Minuten sind es noch 55cm a) Stelle die Funktionsgleichung für die Wasserhöhe auf und fertige eine Skizze des Funktionsgraphen an. b) Bestimme den Zeitpunkt, in dem das Wasser vollständig abgelaufen ist. c) Zu welchem Zeitpunkt beträgt die Wasserhöhe 51cm?
|
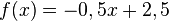 und
und 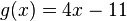
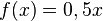 und
und 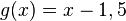
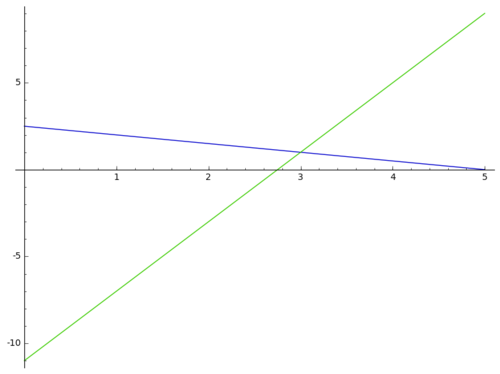
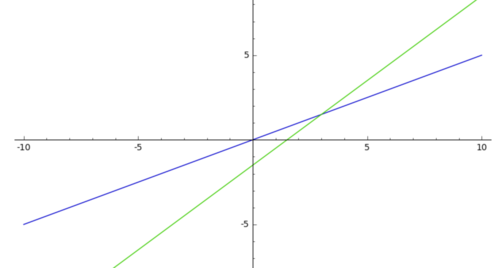
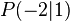 und
und 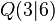
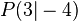 und
und 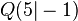
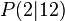 und
und 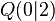
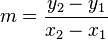
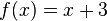
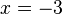
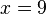
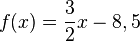
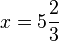
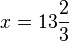
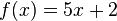
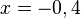
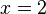
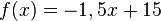
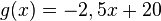
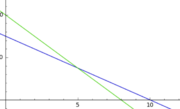
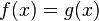
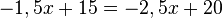
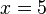 Nach 5 Stunden sind sie gleich lang.
Nach 5 Stunden sind sie gleich lang.