Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Differenzen- und Differenzialquotienten verstehen und inhaltlich deuten
|
Der folgende Lernpfad hilft dir, dein Wissen über den Differenzial- und den Differenzenquotienten aufzufrischen.
Viel Spaß beim Bearbeiten der Aufgaben! :) |
Inhaltsverzeichnis |
Umgang mit den Begriffen Differenzen- und Differenzialquotient
|
|
Differenzen- und Differenzialquotient im Sachkontext
Sachkontextaufgabe Alkoholgehalt
|
|
Brauchst du Hilfe? Dann klicke hier:
Hier findest du die Lösungen:
Sachkontextaufgabe Besucherzahl im Bundestag
|
Die nachfolgende Tabelle stellt die Besucherzahlen zwischen 10.00 Uhr und 18.00 Uhr dar: { |
|
|
|
Deine nächste Aufgabe ist mithilfe des Graphen ungefähr zu bestimmen in welchen Zeitintervallen die Besucherzahlen zu- sowie abnehmen. Notiere die Lösung auf einem Zettel.
Brauchst du einen Tipp? Dann klicke hier: Vergleiche deine Lösung hier: |
|
Brauchst du einen Tipp? Dann klicke hier: Vergleiche deine Lösung hier: |
Sachkontextaufgabe Studenten und Geschwindigkeit
Schaue dir die vier Graphen an und beantworte mithilfe des Differenzen- und Differentialquotienten die anschließenden Fragen
|
|
Rechenbeispiel (Förderaufgabe)
|
Die Menge |
|
Bestimme mit Hilfe vom Differenzenquotienten, wie stark die Nachfrage sinkt, wenn der Preis von 10€ auf 12€ bzw. von 15€ auf 20€ erhöht wird. Wie hoch ist in beiden Fällen die Abnahme je € Preissteigerung? Rechne die Lösung dazu zuerst in deinem Heft aus. Danach kannst du sie in die Felder unten eintragen und überprüfen, ob die Lösung stimmt.
|
|
Mit welchem Nachfragerückgang muss man bei einem Preis von 8€ (15€, 20€) rechnen? Bei welchem Preis ist die Ware unverkäuflich? Rechne auch hier zuerst in deinem Heft. Danach kannst du die Lösung in die Felder unten eintragen und überprüfen, ob sie stimmt.
|
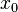
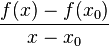
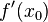
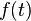 eine Funktion mit
eine Funktion mit 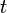 = Zeit in Stunden und
= Zeit in Stunden und 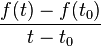 . Da
. Da 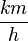
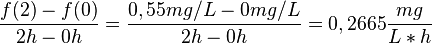 .
.
![[0,2]](/images/math/7/0/f/70fd3f388413505934da60b43afc4088.png) .
.
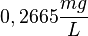 pro Stunde zu.
pro Stunde zu.
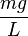 pro Stunde ).
pro Stunde ).
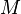 einer bestimmten Ware, die zum Preis
einer bestimmten Ware, die zum Preis 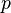 verkauft werden kann, lässt sich durch folgende Beziehung beschreiben:
verkauft werden kann, lässt sich durch folgende Beziehung beschreiben:
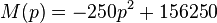 . Je größere Werte die Funktion
. Je größere Werte die Funktion 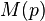 annimmt, desto höher ist also die Nachfrage der Konsumenten zu dieser Ware.
annimmt, desto höher ist also die Nachfrage der Konsumenten zu dieser Ware.
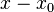 zu teilen (im Beispiel (12-10)). Somit ergibt sich für die Lücken:\\
zu teilen (im Beispiel (12-10)). Somit ergibt sich für die Lücken:\\
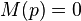 gilt. Die Gleichung muss dann nach
gilt. Die Gleichung muss dann nach 
