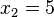Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Terme und Gleichungen: Unterschied zwischen den Versionen
| Zeile 99: | Zeile 99: | ||
c) <math>7y^2+6+4y^2-14x^2-6x^2</math> | c) <math>7y^2+6+4y^2-14x^2-6x^2</math> | ||
| − | <popup name="Tipp">Vorfaktoren einer Variable mit unterschiedlichen Exponenten dürfen <span style="color: red">nicht</span> verrechnet werden! ''Beispiel:'' <math>7x^2+2x+4x=7x^2+6x</math>.</popup> | + | <popup name="Tipp">Vorfaktoren einer Variable mit unterschiedlichen Exponenten dürfen <span style="color: red">'''nicht'''</span> verrechnet werden! ''Beispiel:'' <math>7x^2+2x+4x=7x^2+6x</math>.</popup> |
<popup name="Lösung">a) <math>16x^2+6y</math> | <popup name="Lösung">a) <math>16x^2+6y</math> | ||
| Zeile 118: | Zeile 118: | ||
c) <math>3 (11-7y)</math> | c) <math>3 (11-7y)</math> | ||
| − | <popup name="Tipp 1">Steht in der Klammer eine Addition, so multipliziere den Faktor vor der Klammer mit jedem Summanden in der Klammer. Bei der Subtraktion geht es genau so. ''Beispiel:'' <math>6 \cdot (6+9) = 6 \cdot 6 + 6 \cdot 9 = 36+54 = 90</math>. | + | <popup name="Tipp 1">Steht in der Klammer eine Addition, so multipliziere den Faktor vor der Klammer mit jedem Summanden in der Klammer. Bei der Subtraktion geht es genau so. ''Beispiel:'' <math>{\color{blue}6} \cdot ({\color{red}6}+{\color{green}9}) = {\color{blue}6} \cdot {\color{red}6} + {\color{blue}6} \cdot {\color{green}9} = 36+54 = 90</math>. Dieser Tipp geht auf das Distributivgesetz zurück.</popup> |
<popup name="Tipp 2">zu c): Ist kein Rechenzeichen explizit vor die Klammer geschrieben, so ist die Multiplikation gemeint.</popup> | <popup name="Tipp 2">zu c): Ist kein Rechenzeichen explizit vor die Klammer geschrieben, so ist die Multiplikation gemeint.</popup> | ||
<popup name="Lösung">a) <math>4x+20</math> | <popup name="Lösung">a) <math>4x+20</math> | ||
| Zeile 173: | Zeile 173: | ||
<popup name="Tipp 1">Du kannst hier die binomischen Formeln anwenden. <math>(a+b)^2=a^2+2ab+b^2</math> und <math>(a-b)^2=a^2-2ab+b^2</math>. Die binomischen Formeln gehen auf die doppelte Anwendung des Distributivgesetzes zurück.</popup> | <popup name="Tipp 1">Du kannst hier die binomischen Formeln anwenden. <math>(a+b)^2=a^2+2ab+b^2</math> und <math>(a-b)^2=a^2-2ab+b^2</math>. Die binomischen Formeln gehen auf die doppelte Anwendung des Distributivgesetzes zurück.</popup> | ||
<popup name="Tipp 2">Statt die binomischen Formeln anzuwenden, kannst du die Klammer auch per Hand ausmultiplizieren. Der Exponent <math>()^2</math> bedeutet, dass die Klammer mit sich selbst multipliziert werden soll. ''Beispiel:'' <math>(x+3)^2=(x+3) \cdot (x+3)</math>.</popup> | <popup name="Tipp 2">Statt die binomischen Formeln anzuwenden, kannst du die Klammer auch per Hand ausmultiplizieren. Der Exponent <math>()^2</math> bedeutet, dass die Klammer mit sich selbst multipliziert werden soll. ''Beispiel:'' <math>(x+3)^2=(x+3) \cdot (x+3)</math>.</popup> | ||
| − | <popup name="Tipp 3">Beim Multiplizieren von zwei Klammern, muss jeder Summand mit jedem Summanden multipliziert werden. ''Beispiel:'' <math>(x+3) \cdot (x+3) = x \cdot x + x \cdot 3 + 3 \cdot x + 3 \cdot 3 = x^2+3x+3x+9 = x^2+6x+9</math>. Diese Regel geht auf die doppelte Anwendung des Distributivgesetzes zurück.</popup> | + | <popup name="Tipp 3">Beim Multiplizieren von zwei Klammern, muss jeder Summand mit jedem Summanden multipliziert werden. ''Beispiel:'' <math>({\color{blue}x}+{\color{red}3}) \cdot ({\color{Orange}x}+{\color{green}3}) = {\color{blue}x} \cdot ({\color{Orange}x}+{\color{green}3}) + {\color{red}3} \cdot ({\color{Orange}x}+{\color{green}3}) = {\color{blue}x} \cdot {\color{Orange}x} + {\color{blue}x} \cdot {\color{green}3} + {\color{red}3} \cdot {\color{Orange}x} + {\color{red}3} \cdot {\color{green}3} = x^2+3x+3x+9 = x^2+6x+9</math>. Diese Regel geht auf die doppelte Anwendung des Distributivgesetzes zurück.</popup> |
<popup name="Lösung">a) <math>16x^2+40x+25</math> | <popup name="Lösung">a) <math>16x^2+40x+25</math> | ||
| Zeile 228: | Zeile 228: | ||
b) <math>0=x^2+13x</math> | b) <math>0=x^2+13x</math> | ||
| − | c) <math>- | + | c) <math>-2x=\frac{1}{2}x^2</math> |
<popup name="Tipp 1">zu a): Bei Gleichungen der Form <math>ax^2+c</math>, also ohne linearen Summanden <math>bx</math> kannst du die Gleichung umstellen, sodass <math>x^2</math> alleine steht und anschließend die Wurzel ziehen.</popup> | <popup name="Tipp 1">zu a): Bei Gleichungen der Form <math>ax^2+c</math>, also ohne linearen Summanden <math>bx</math> kannst du die Gleichung umstellen, sodass <math>x^2</math> alleine steht und anschließend die Wurzel ziehen.</popup> | ||
<popup name="Tipp 2">zu a): Achte beim Wurzelziehen auf die positive und negative Lösung.</popup> | <popup name="Tipp 2">zu a): Achte beim Wurzelziehen auf die positive und negative Lösung.</popup> | ||
<popup name="Tipp 3">zu b): Bei Gleichungen der Form <math>ax^2+bx</math>, also ohne konstanten Summanden <math>c</math> kannst du <math>x</math> ausklammern.</popup> | <popup name="Tipp 3">zu b): Bei Gleichungen der Form <math>ax^2+bx</math>, also ohne konstanten Summanden <math>c</math> kannst du <math>x</math> ausklammern.</popup> | ||
| − | <popup name="Tipp 4">zu b): Ein Produkt ist genau dann <math>0</math>, wenn einer der beiden Faktoren bereits <math>0</math> ist. ''Beispiel:'' <math>x \cdot (x-2)=0</math> bedeutet, dass entweder <math> | + | <popup name="Tipp 4">zu b): Ein Produkt ist genau dann <math>0</math>, wenn einer der beiden Faktoren bereits <math>0</math> ist. ''Beispiel:'' <math>{\color{blue}x} \cdot ({\color{red}x-2})=0</math> bedeutet, dass entweder <math>{\color{blue}x}=0</math> oder <math>{\color{red}x-2}=0</math> gilt.</popup> |
| − | <popup name="Tipp 5">zu c): Stelle um, sodass auf einer Seite des Gleichheitszeichen <math>0</math> steht | + | <popup name="Tipp 5">zu c): Stelle um, sodass auf einer Seite des Gleichheitszeichen <math>0</math> steht.</popup> |
<popup name="Lösung">a) <math>x_1=-8</math> oder <math>x_2=8</math> | <popup name="Lösung">a) <math>x_1=-8</math> oder <math>x_2=8</math> | ||
Version vom 30. Mai 2018, 18:17 Uhr
|
In diesem Lernpfad geht es um das Wiederhohlen und Vertiefen deines Wissens über Terme und Gleichungen. Du findest hier Übungsaufgaben zu den Themen Terme aufstellen, Terme umformen und Gleichungen Lösen. Der Lernpfad orientiert sich dabei an der Tabelle zur Selbsteinschätzung des Diagnosetests Matematik zum Übergang SI / SII, sodass du gezielt die Aufgaben bearbeiten kannst, bei denen du dich noch verbessern möchtest. Solltest du bei einer Aufgabe nicht weiterkommen, findest du unter dieser verschiedene Tipps, die dir helfen könnten. Versuche die Aufgabe jedoch zunächst ohne Hilfe zu bearbeiten; klappt dies nicht oder stimmt deine Lösung nicht mit der angegebenen Lösung überein, so kannst du dir nacheinander die Tipps anschauen. Falls es mehrere Tipps gibt, starte damit dir Tipp 1 anzuschauen und versuche dann zunächst wieder die Aufgabe zu lösen, usw. |
Inhaltsverzeichnis |
Terme aufstellen
|
Klicke alle Terme an, die den Flächeninhalt der Fläche beschreiben.
|
|
Eine Kerze ist 15 cm hoch und brennt pro Stunde 3,5 cm ab. Stelle einen Term auf, mit dem du die Höhe der Kerze zu einem beliebigen Zeitpunkt berechnen kannst. |
|
Einem Patienten soll nach einer Operation innerhalb von 8 Stunden 100 ml Infusionslösung über einen Tropf verabreicht werden. Innerhalb der ersten vier Stunden laufen bereits 40 ml durch den Tropf. Um die restlichen 60 ml in den verbleibenden vier Stunden zu verabreichen wird die Tropfgeschwindigkeit auf 15 ml pro Stunde erhöht. Stelle einen Term für das Volumen der bereits verabreichten Infusionslösung ab 4 Stunden auf. |
Terme zusammenfassen
|
Fasse die Terme zusammen. a) b) c) |
|
Fasse die Terme zusammen. a) b) c) |
|
Fasse die Terme zusammen. a) b) c) |
|
Fasse die Terme zusammen. a) b) c) |
Klammern in Termen auflösen
|
Löse die Klammern auf. a) b) c) |
|
Löse die Klammern auf. a) b) c) |
|
Löse die Klammern auf. a) b) c) |
|
Löse die Klammern auf. a) b) c) |
In Termen ausklammern
|
Ordne die Paare zu.
|
|
Klammere soweit wie möglich aus. a) b) c) |
Lineare Gleichungen lösen
|
Löse die linearen Gleichungen.
|
Quadratische Gleichungen lösen
|
Löse die quadratischen Gleichungen ohne p-q-Formel. a) b) c) |
|
Löse die quadratischen Gleichungen. a) b) c) |
|
Löse die quadratischen Gleichungen. a) b) c) |
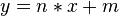 , wobei n die Steigung und m der y-Achsenabschnitt ist. Welche Bedeutung haben diese im Sachzusammenhang?
, wobei n die Steigung und m der y-Achsenabschnitt ist. Welche Bedeutung haben diese im Sachzusammenhang?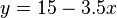 , wobei
, wobei 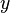 die Höhe in Zentimetern und
die Höhe in Zentimetern und 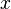 die Zeit in Stunden ist.
die Zeit in Stunden ist.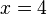 aufweisen?
aufweisen?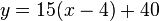
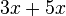
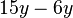
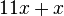
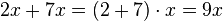 . Dieser Tipp geht auf das Distributivgesetz zurück.
. Dieser Tipp geht auf das Distributivgesetz zurück.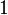 wird in der Regel nicht ausgeschrieben. Steht also kein Faktor vor einer Variablen, so handelt es sich um
wird in der Regel nicht ausgeschrieben. Steht also kein Faktor vor einer Variablen, so handelt es sich um 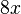
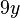
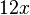
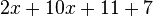
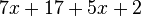
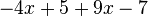
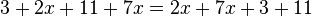 . Dieser Tipp geht auf das Kommutativgesetz zurück, welches bei der Addition gilt. Jede Subtraktion
. Dieser Tipp geht auf das Kommutativgesetz zurück, welches bei der Addition gilt. Jede Subtraktion 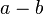 kann zudem in eine Addition umgeformt werden
kann zudem in eine Addition umgeformt werden 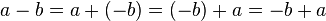 .
.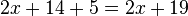 .
.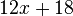
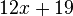
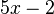
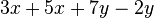
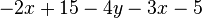
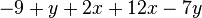
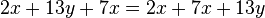 . Dieser Tipp geht auf das Kommutativgesetz zurück, welches bei der Addition gilt. Jede Subtraktion
. Dieser Tipp geht auf das Kommutativgesetz zurück, welches bei der Addition gilt. Jede Subtraktion 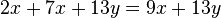 . Diese Regel geht auf das Distributivgesetz zurück, indem die Variable ausgeklammert wird.
. Diese Regel geht auf das Distributivgesetz zurück, indem die Variable ausgeklammert wird.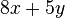
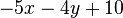
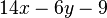
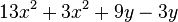
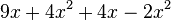
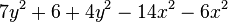
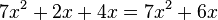 .
.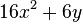
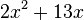
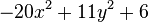
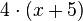
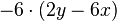
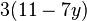
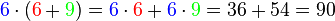 . Dieser Tipp geht auf das Distributivgesetz zurück.
. Dieser Tipp geht auf das Distributivgesetz zurück.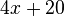
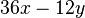
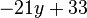
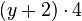
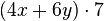
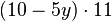
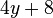
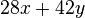
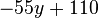
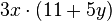
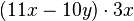
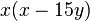
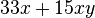
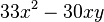
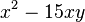
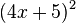
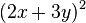
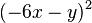
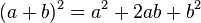 und
und 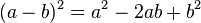 . Die binomischen Formeln gehen auf die doppelte Anwendung des Distributivgesetzes zurück.
. Die binomischen Formeln gehen auf die doppelte Anwendung des Distributivgesetzes zurück.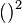 bedeutet, dass die Klammer mit sich selbst multipliziert werden soll. Beispiel:
bedeutet, dass die Klammer mit sich selbst multipliziert werden soll. Beispiel: 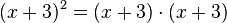 .
.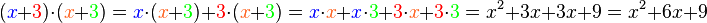 . Diese Regel geht auf die doppelte Anwendung des Distributivgesetzes zurück.
. Diese Regel geht auf die doppelte Anwendung des Distributivgesetzes zurück.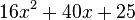
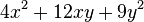
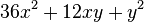
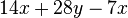
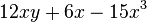
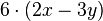
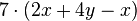
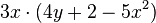
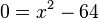
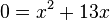
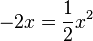
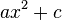 , also ohne linearen Summanden
, also ohne linearen Summanden 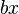 kannst du die Gleichung umstellen, sodass
kannst du die Gleichung umstellen, sodass 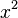 alleine steht und anschließend die Wurzel ziehen.
alleine steht und anschließend die Wurzel ziehen.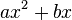 , also ohne konstanten Summanden
, also ohne konstanten Summanden  kannst du
kannst du 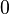 , wenn einer der beiden Faktoren bereits
, wenn einer der beiden Faktoren bereits 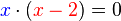 bedeutet, dass entweder
bedeutet, dass entweder 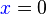 oder
oder 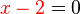 gilt.
gilt.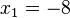 oder
oder 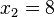
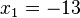 oder
oder 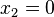
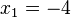 oder
oder 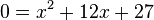
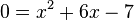
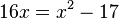
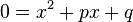 , lies dann
, lies dann 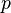 und
und 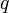 ab und bestimme die Lösung mit
ab und bestimme die Lösung mit 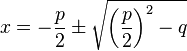 .
.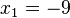 oder
oder 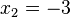
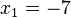 oder
oder 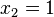
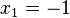 oder
oder 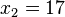
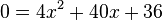
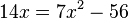
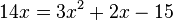
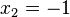
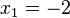 oder
oder