Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Die Ableitung im Sachkontext anwenden
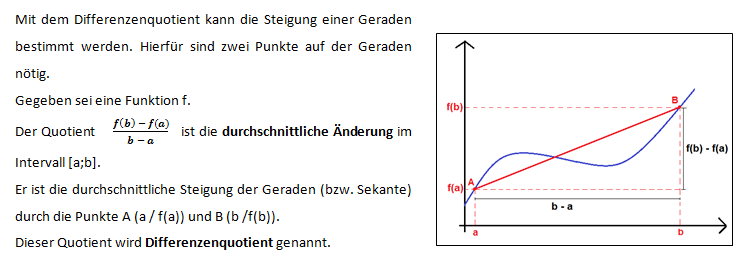
30px Merke
Die Aufgaben auf dieser Seite unterscheiden sich in ihrem Lernschwerpunkt und Schwierigkeitsgard:
|
Inhaltsverzeichnis |
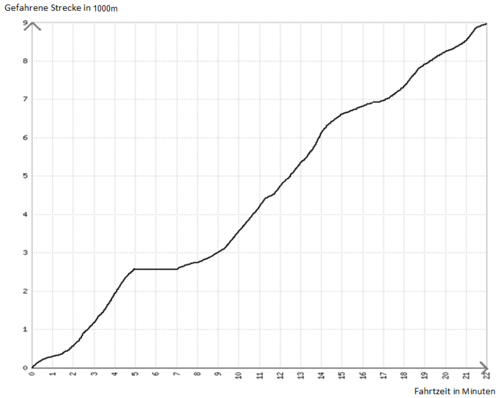
Aufgabe 1: Fahrtenschreiber
|
Herr Müller arbeitet als Testfahrer bei einem Autohersteller. Seit zwei Tagen fährt und testet er einen neuen spritsparenden Prototypen. |
a) Wie schnell ist Herr Müller auf seinem Weg zur Arbeit im Durchschnitt gefahren?
Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist. Gib die Lösung mit einer Nachkommastelle an!
Bei Problemen, klicke auf die Glühbirne oben links.
b) Auf seinem Weg musst Herr Müller vor einer roten Ampel warten. Wann war das?
Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist.
c) Beschreibe den Fahrtverlauf der ersten 12 Minuten stichpunktartig.
Aufgabe 2: Ballwurf
|
Bei den Bundesjugendspielen der Klasse 9 wirft Lisa einen Ball. Die Flugkurve ihres Balls kann näherungsweise durch die Funktion |
a) Den Flug des Balls kannst du unter folgendem Link genauer betrachten. Lass hierzu den roten Ball fliegen, indem du bei dem roten Ball auf play drücken. Die anderen Punkte solltest du nicht bewegen!
b) Bestimme die Steigung des Balls an den verschiedenen Punkten der Flugkurve.
c) Ordne die mathematischen Begriffe und Interpretationen den Markierungen auf dem Graphen zu.
Die gelbe Markierung soll einen Bereich statt einen Punkt kennzeichnen.
Für die Zuordnung musst die verschiedenen Markierungen anklicken und anschließend eine der vorgeschlagenen Möglichkeiten auswählen.
d) Fülle die Lücken, indem du die Aufgabe im Sachzusammenhang interpretieren.
Aufgabe 3: Zuordnungen
|
Ordne den Abbildungen oder Formeln die zugehörige Interpretation zu |
Aufgabe 4: Baumwachstum
|
Befasse dich mit der folgenden Anwendungsaufgabe. Nimm dazu dein Heft für die Rechnungen zur Hilfe
|
a) Berechne den Funktionswert von f an der Stelle t=30 und interpretiere das Ergebnis im Sachzusammenhang.
b) Bestimme rechnerisch das Alter, in dem die Fichte am stärksten wächst, und gib die größte Wachstumsgeschwindigkeit an.
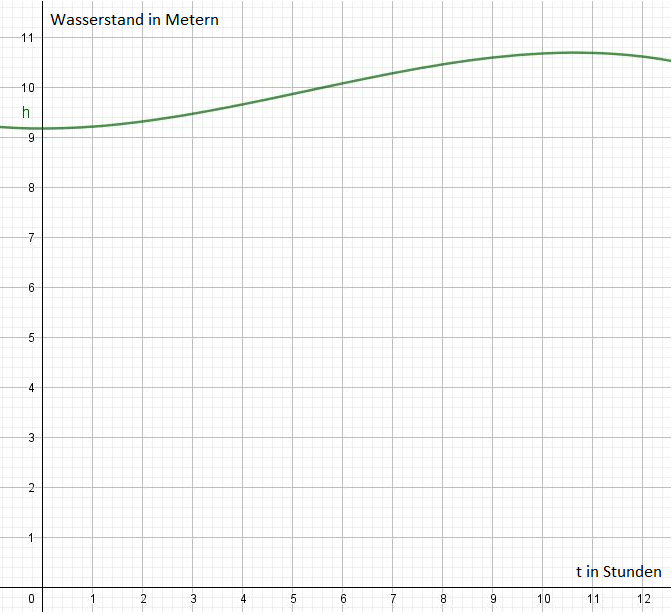
Aufgabe 5: Wasserstand
|
Befasse dich mit der folgenden Anwendungsaufgabe. Nimm dazu dein Heft für die Rechnungen zur Hilfe
|
a) Berechne die Höhe des Wasserstandes um 7:30 Uhr.
b) Berechne die Geschwindigkeit, mit der der Wasserstand in den ersten acht Stunden des Beobachtungszeitraumes durchschnittlich anstieg.
c) Ermittle den Zeitpunkt,an dem der höchste Wasserstand an der Messtation erreicht wurde. Bereche auch den exakten Höchststand.
d) Bestimme rechnerisch den Zeitpunkt, zu dem der Wasserstand am schnellsten anstieg, rechnerisch.
Aufgabe 6: Nutzungsverhalten
|
In den letzten 24 Stunden hat eine Internetseite erfasst, wie viele Besucher die Seite hatte. Die Abbildung zeigt das Nutzungsverhalten von 6 bis 20 Uhr Nutzungsverhalten der Internetseite |
a) Wie viele Besucher hatte die Internetseite um 10 Uhr?
Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist. Gib die Lösung mit einer Nachkommastelle an!
Bei Problemen, klicke auf die Glühbirne oben links.
b) Wie viele Nutzer sind von 8 bis 10 Uhr im Durchschnitt pro Stunde dazu gekommen?
Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist.
Bei Problemen, klicke auf die Glühbirne oben links.
c) Zu welchem Zeitpunkt hat sich die Bescuherzahl durchschnittlich am stärksten geändert?
Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist. Gib die Lösung mit einer Nachkommastelle an!
Bei Problemen, klicke auf die Glühbirne oben links.
d) Zu welcher Uhrzeit haben die meisten Besucher die Internetseite besucht?
Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist. Gib die Lösung mit einer Nachkommastelle an!
Bei Problemen, klicke auf die Glühbirne oben links.
Aufgabe 7: Konzertkarten
|
Befasse dich mit der folgenden Anwendungsaufgabe. Nimm dazu dein Heft für die Rechnungen zur Hilfe
|
a) Zu welchem Zeitpunkt werden die meisten Karten pro Minute verkauft?
b) Wann im Verlauf der ersten Stunde nimmt die Anzahl der verkauften Karten am schnellsten ab?
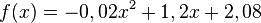 beschrieben werden.
beschrieben werden.
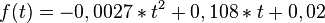 wird das Wachstum einer Fichte in Abhängigkeit von der Zeit t (in Jahren) beschrieben. Dabei gibt f(t) die Wachstumsgeschwindigkeit in Metern pro Jahr an. Zum Zeitpunkt t=0 hat eine frisch eingepflanzte Fichte eine Höhe von ca. 20 cm.
wird das Wachstum einer Fichte in Abhängigkeit von der Zeit t (in Jahren) beschrieben. Dabei gibt f(t) die Wachstumsgeschwindigkeit in Metern pro Jahr an. Zum Zeitpunkt t=0 hat eine frisch eingepflanzte Fichte eine Höhe von ca. 20 cm.

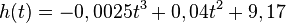
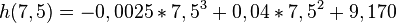 =...≈
=...≈ 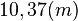
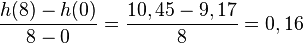 . Die Geschwindigkeit in den ersten achten Stunden betrug durchschnittlich 0,16 m/h.
. Die Geschwindigkeit in den ersten achten Stunden betrug durchschnittlich 0,16 m/h. 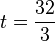 ≈ 10,67 (und t=0, entfällt, da h"(0)>0 und somit wäre es ein Tiefpunkt. (Dieser ist jedoch nicht gesucht.) Der Hochpunkt lautet H(32/3 | 5771/540). Der Wasserstand liegt bei etwa 10,69 m um etwa 10:40 Uhr.
≈ 10,67 (und t=0, entfällt, da h"(0)>0 und somit wäre es ein Tiefpunkt. (Dieser ist jedoch nicht gesucht.) Der Hochpunkt lautet H(32/3 | 5771/540). Der Wasserstand liegt bei etwa 10,69 m um etwa 10:40 Uhr. 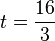 . Daraus folgt, dass der Wasserstand nach 5 Stunden und 20 Minuten am schnellsten anstieg.
. Daraus folgt, dass der Wasserstand nach 5 Stunden und 20 Minuten am schnellsten anstieg. 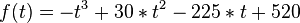 für 6 ≤ t ≤ 20 wird das Nutzungsverhalten von 6 bis 20 Uhr dargestellt.
für 6 ≤ t ≤ 20 wird das Nutzungsverhalten von 6 bis 20 Uhr dargestellt. 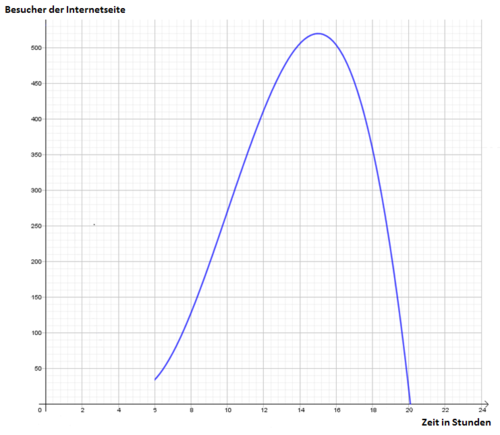
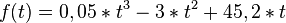 beschreibt näherungsweise die Anzahl der Karten, die pro Minute zu einer bestimmten Zeit verkauft werden für die ersten dreißig Minuten des Verkaufs t=0 steht für den Zeitpunkt der Freischaltung der Hotline.
beschreibt näherungsweise die Anzahl der Karten, die pro Minute zu einer bestimmten Zeit verkauft werden für die ersten dreißig Minuten des Verkaufs t=0 steht für den Zeitpunkt der Freischaltung der Hotline.

