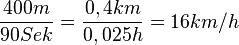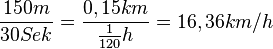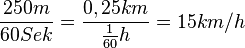Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Von der mittleren zur momentanen (lokalen) Änderungsrate
Inhaltsverzeichnis[Verbergen] |
|
Dieser Lernpfad beschäftigt sich mit der durchschnittlichen und der momentanen Änderungsrate.
|
Die durchschnittliche Änderungsrate
| In dieser Aufgabe erwarten dich drei Teilaufgaben. In der ersten geht es um die Berechnung der durchschnittlichen Änderungsrate. Solltest du da bereits sicher sein, kannst du dich auf 4. und 5. konzentrieren und direkt zu Teil b) übergehen, in dem ein Ergebnis aus a) erklärt werden soll. In Teil c) sollen einem Diagramm Informationen entnommen werden. |
|
Wie groß ist die durchschnittliche Änderungsrate für ...
|
Wie ist der zweite Wert (Ergebnis) bei a) 1. zu erklären?
|
|
Unterscheidung von durchschnittlicher und momentaner Änderungsrate
| In dieser Aufgabe erwarten dich zwei Teilaufgaben. In der ersten kannst du trainieren, wann die durchschnittliche und wann die momentane Änderungsrate zu berechnen ist. In Teilaufgabe b) wird das Erlernte dann vertieft. Diese Teilaufgabe ist besonders geeignet, wenn du in Teilaufgabe a) sehr sicher warst und danach eine Herausforderung suchst. |
|
|
|
Formuliere in deinem Heft, woran du die Entscheidung für die momentane oder durchschnittliche Änderungsrate festmachst! |
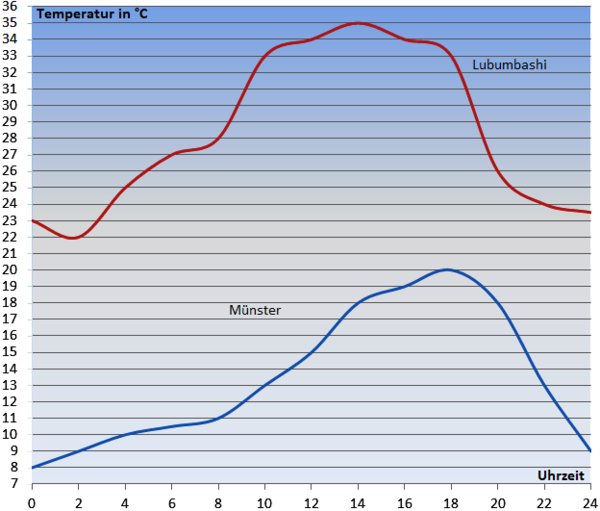
Von der durchschnittlichen zur momentanen Änderungsrate - eine Fahrradtour durch Münster
| In dieser Aufgabe erwarten dich fünf Teilaufgaben. In der ersten sollst du zunächst aus einem Video Daten extrahieren. In den Teilaufgaben b) und c) sollen dann anhand dieser Daten durchschnittliche Änderungsraten berechnet werden. In Teilaufgabe d) kannst du überprüfen, wie gut du die Bedeutung der durchschnittlichen Änderungsrate schon verstanden hast. In der letzten Teilaufgabe kannst du dann selber graphisch ausprobieren, wie aus der durchschnittlichen Änderungsrate die momentane Änderungsrate wird.
|
|
Eine Gruppe Touristen macht eine Sightseeing-Tour mit dem Fahrrad durch Münster. Sie starten in der Nähe von Münsters Schloss. Nachfolgend siehst du eine Video-Aufnahme, die einer der Touristen auf der Tour aufnimmt. Übertrage folgende Tabelle in dein Heft: |
| Nr. | Streckenabschnitt | Zeit (Sek) | Entfernung (m) |
|---|---|---|---|
| 1 | Beginn der Aufnahme in der Frauenstraße | 0 | |
| 2 | Abbiegen auf den Rad- & Fußweg an der eingerüsteten Überwasserkirche | 150 | |
| 3 | Ankunft am Dom | 400 |
Sieh dir nun das Video an und notiere in der dritten Spalte die Zeit im Video, an der die Streckenabschnitte der zweiten Spalte beginnen.
Hinweis: Die Zeitangaben sind hier nicht ganz eindeutig. Du kannst dich auf eine Zeit festlegen, denn es ist für die weitere Aufgabe nicht entscheidend, ob die Radfahrer schon eine Sekunde früher oder später an einem Ort angekommen sind.
|
Berechne die durchschnittliche Geschwindigkeit, mit der die Touristen die gesamte Strecke von Beginn der Aufnahme bis zum Dom zurückgelegt haben. |
|
Wie schnell waren die Touristen im Schnitt zwischen
|
|
Beantworte die folgenden Fragen. |
Halten sich die Touristen zwischen Beginn der Aufnahme und dem Abbiegen auf den Fuß- & Radweg an der eingerüsteten Überwasserkirche an die Schrittgeschwindigkeit von 6km/h?
Wenn die durchschnittliche Geschwindigkeit der Radfahrer für die Strecke über 6km/h liegt, dann halten sie sich in keinem Teilbereich der Strecke an die Schrittgeschwindigkeit. Stimmt diese Aussage?
|
In dem Video habt ihr unter anderem gesehen, wie die Radfahrer nach ca. 33 Sekunden von der Straße auf den Fuß- und Radweg an der Überwasserkirche abbiegen. Diesen Vorgang seht ihr in dem untenstehenden Applet: Die blaue Funktion h gibt auf der x-Achse die benötigte Zeit in Sekunden und auf der y-Achse die zurückgelegte Strecke in Metern an. Der Punkt P liegt bei 33 Sekunden, also genau im Abbiegevorgang. Die rote Funktion f ist die Sekante durch den Punkt P und einen Punkt Q, den ihr über den schwarzen Schieberegler verschieben könnt. Ihr könnt darüber also den Bereich auswählen, in dem die Durchschnittsgeschwindigkeit m angegeben werden soll. Wie schnell sind die Radfahrer in dem Moment des Abbiegens bei 33 Sekunden? Begründe deine Antwort in deinem Heft mithilfe des Applets. |
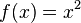 im Intervall
im Intervall ![[3, 5]](/images/math/f/5/3/f53af11412591f12d4a404e2de96a921.png) und im Intervall
und im Intervall ![[-1, 1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) ?
?
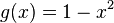 im Intervall
im Intervall ![[1, 3]](/images/math/6/8/9/689e1b934020b6eb3917c155d94a9a0f.png) ?
?
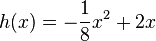 im Intervall
im Intervall ![[2, 10]](/images/math/6/1/3/613a967f3ed17bd82cab639e20e50336.png) ?
?
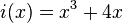 im Intervall
im Intervall ![[-5, 6]](/images/math/2/0/8/20870f49669554d5c486381fc331b35c.png) ?
?
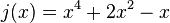 im Intervall
im Intervall ![[-6, -2]](/images/math/8/6/e/86efb2eb99cd613873958bfdb84a8f44.png) ?
?
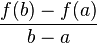 wird Differenzenquotient genannt. Dieser Quotient beschreibt, wie groß der Unterschied zwischen den Werten der Funktion an den Intervallgrenzen
wird Differenzenquotient genannt. Dieser Quotient beschreibt, wie groß der Unterschied zwischen den Werten der Funktion an den Intervallgrenzen 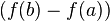 im Verhältnis zu der Länge des Intervalls
im Verhältnis zu der Länge des Intervalls 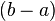 ist. Damit entspricht dieser Quotient der Steigung der Geraden (Sekanten) durch die Punkte
ist. Damit entspricht dieser Quotient der Steigung der Geraden (Sekanten) durch die Punkte 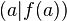 und
und 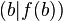 .
.