Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Verhalten nahe 0 und gegen +- Unendlich
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
|
|
|
|
|
Gegeben ist die Funktion f mit |
Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0. a)
b)
c)
|
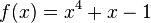 hat als höchsten Exponenten 4, verhält sich also gegen Unendlich wie
hat als höchsten Exponenten 4, verhält sich also gegen Unendlich wie 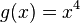 . Also geht sie für x gegen - Unendlich gegen + Unendlich und für x gegen + Unendlich auch gegen + Unendlich.
Die Funktion verhält sich nahe 0 wie der x-Wert mit dem kleinsten Exponenten und dem absoluten Glied, also wie
. Also geht sie für x gegen - Unendlich gegen + Unendlich und für x gegen + Unendlich auch gegen + Unendlich.
Die Funktion verhält sich nahe 0 wie der x-Wert mit dem kleinsten Exponenten und dem absoluten Glied, also wie 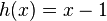 . Damit ist es nahe 0 annähernd eine Gerade, die die Steigung 1 und den y-Achsenabschnitt -1 hat.
. Damit ist es nahe 0 annähernd eine Gerade, die die Steigung 1 und den y-Achsenabschnitt -1 hat.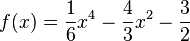 . Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0.
. Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0.
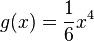 . Also gilt sowohl für x->-∞ als auch für x->∞ f(x)->∞. Für x nahe 0 verhält sich der Graph der Funktion f wie Fehler beim Parsen(Lexikalischer Fehler): h(x)=-\frac{4}{3}x^2-\frac{3}{2}. Der Graph sieht also wie eine nach unten geöffnete und um 1,5 nach unten verschobene Parabel aus.
. Also gilt sowohl für x->-∞ als auch für x->∞ f(x)->∞. Für x nahe 0 verhält sich der Graph der Funktion f wie Fehler beim Parsen(Lexikalischer Fehler): h(x)=-\frac{4}{3}x^2-\frac{3}{2}. Der Graph sieht also wie eine nach unten geöffnete und um 1,5 nach unten verschobene Parabel aus.
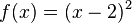
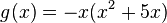
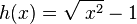
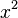 , also x--> -∞ = ∞
, also x--> -∞ = ∞ 
