Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Mathematik Klasse 9
Auf dieser Seite sollen quadratische Funktionen untersucht werden.
Inhaltsverzeichnis |
Einführung
Wir haben im Unterricht quadratische Funktionen der Form 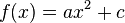 kennen gelernt.
Dabei ist x die Variable, die alle Zahlen durchläuft. a und c sind Parameter und stehen für einzelne Werte, die man einsetzt, und damit jeweils eine spezielle quadratische Funktion erhält. Für
kennen gelernt.
Dabei ist x die Variable, die alle Zahlen durchläuft. a und c sind Parameter und stehen für einzelne Werte, die man einsetzt, und damit jeweils eine spezielle quadratische Funktion erhält. Für 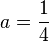 und
und 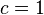 erhält man die Funktion
erhält man die Funktion 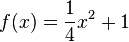 . Für
. Für 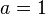 und
und 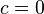 erhält man die einfachste quadratische Funktion
erhält man die einfachste quadratische Funktion 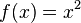 , deren Graph die Normalparabel ist.
, deren Graph die Normalparabel ist.
Im Folgenden soll untersucht werden, wie sich eine Veränderung der Parameter a und c auf den Graphen auswirkt.
Der Parameter a
Wir betrachten zunächst nur den Parameter a und untersuchen 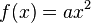 .
.
Im Applet ist zunächst a=1 gesetzt, also die Normalparabel eingezeichnet. Mit Hilfe des Schiebereglers kannst du den Parameter ändern.
|
a) Untersuche , was passiert, wenn du a änderst. |
Der Parameter c
Wir betrachten zunächst nun den Parameter c und untersuchen 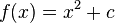 .
.
Im Applet
ist zunächst c=0 gesetzt, also die Normalparabel eingezeichnet.
Mit Hilfe des Schiebereglers kannst du den Parameter ändern.
|
a) Untersuche , was passiert, wenn du c änderst. |
Kombination
Im Im Applet kannst du beide Parameter ändern.
|
a) Für welchen Wert von a geht der Graph von |
Auf dieser Seite sollen quadratische Funktionen weiter untersucht werden.
Einführung
Wir haben im Unterricht quadratische Funktionen der Form 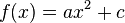 kennen gelernt und untersucht, wie sich eine Veränderung der Parameter a und c auf den Graphen auswirkt. Eine Veränderung des Parameters c bewirkt dabei eine Verschiebung entlang der y-Achse.
kennen gelernt und untersucht, wie sich eine Veränderung der Parameter a und c auf den Graphen auswirkt. Eine Veränderung des Parameters c bewirkt dabei eine Verschiebung entlang der y-Achse.
Jetzt sollen Parabeln etwas allgemeiner betrachtet werden, wir untersuchen quadratische Funktionen der Form 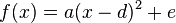
Im Applet
ist zunächst a=1, d=0 und e=0 gesetzt, also die Normalparabel, die zu 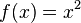 gehört, eingezeichnet.
Mit Hilfe des Schiebereglers kannst du die Parameter ändern.
gehört, eingezeichnet.
Mit Hilfe des Schiebereglers kannst du die Parameter ändern.
|
a) Untersuche , was passiert, wenn du d änderst. |
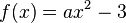 durch den Punkt
durch den Punkt 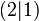 .
. 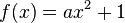 durch den Punkt
durch den Punkt 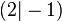 .
. 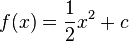 durch den Punkt
durch den Punkt 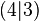 .
. 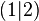 .
.
