Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Benutzer:Tina WWU3: Unterschied zwischen den Versionen
(→Unterscheidung der Änderungsraten) |
(→Unterscheidung der Änderungsraten) |
||
| Zeile 2: | Zeile 2: | ||
{{Aufgaben|2: Unterscheidung der mittleren und lokalen Änderungsrate| | {{Aufgaben|2: Unterscheidung der mittleren und lokalen Änderungsrate| | ||
| − | '''a)''' | + | '''a)''' Ordne die Karten jeweils richtig zu, indem ihr sie entweder zur durchsnittlichen oder lokalen Änderungsrate zieht. |
| − | + | ||
| − | Ordne die Karten jeweils richtig zu, indem ihr sie entweder zur durchsnittlichen oder lokalen Änderungsrate zieht. | + | |
<iframe src="https://learningapps.org/watch?app=764461" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?app=764461" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| Zeile 14: | Zeile 12: | ||
| − | '''b)''' | + | '''b)''' Fertige in deinem Heft eine Tabelle zur durchschnittlichen und momentanen Änderungsrate mit den Karten aus Teilaufgabe a an. Stelle die zueinander passenden Begriffe und Formeln gegenüber, zum Beispiel Sekante und Tangente. |
| − | + | ||
| − | Fertige in deinem Heft eine Tabelle zur durchschnittlichen und momentanen Änderungsrate mit den Karten aus Teilaufgabe a an. Stelle die zueinander passenden Begriffe und Formeln gegenüber, zum Beispiel Sekante und Tangente. | + | |
<popup name="Lösung" | <popup name="Lösung" | ||
>{| class="wikitable" | >{| class="wikitable" | ||
| Zeile 53: | Zeile 49: | ||
<iframe src="https://learningapps.org/watch?v=pg7j9c1ek18" style="border:0px;width:100%;height:300px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=pg7j9c1ek18" style="border:0px;width:100%;height:300px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| − | <popup name="Lösung a)">Nach 3 Sekunden hat Tim einen Weg von 21 Metern zurückgelegt, denn <math>s(3)=10*3-3^2=30-9=21</math>. Nach 5 Sekunden hat er 25 Meter zurückgelegt, denn es gilt s(5)=10*5-5^2=50-25=25.</popup> | + | <popup name="Lösung a)">Nach 3 Sekunden hat Tim einen Weg von 21 Metern zurückgelegt, denn <math>s(3)=10*3-3^2=30-9=21</math>. Nach 5 Sekunden hat er 25 Meter zurückgelegt, denn es gilt <math>s(5)=10*5-5^2=50-25=25</math>.</popup> |
| − | <popup name="Lösung b)">Die momentane Änderungsrate <math>s'(t)=10-2t</math> entspricht der Geschwindigkeit. <math>s'(3)=10- | + | <popup name="Lösung b)">Die momentane Änderungsrate <math>s'(t)=10-2t</math> entspricht der Geschwindigkeit. <math>s'(3)=10-2*3=10-6=4</math> und <math>s'(5)=10-2*5=10-10=0</math>.</popup> |
<popup name="Lösung c)">Die angegebene Formel kann nicht für t=6 gelten, da die gegebene Funktion nur für den Definitionsbereich <math>t\in [0;5]</math> gilt. In der Realität bedeutet es, dass Tim nach 5 Sekunden schon stehen geblieben ist.</popup> | <popup name="Lösung c)">Die angegebene Formel kann nicht für t=6 gelten, da die gegebene Funktion nur für den Definitionsbereich <math>t\in [0;5]</math> gilt. In der Realität bedeutet es, dass Tim nach 5 Sekunden schon stehen geblieben ist.</popup> | ||
}} | }} | ||
Version vom 13. November 2018, 14:11 Uhr
Unterscheidung der Änderungsraten
 Aufgabe 2: Unterscheidung der mittleren und lokalen Änderungsrate
a) Ordne die Karten jeweils richtig zu, indem ihr sie entweder zur durchsnittlichen oder lokalen Änderungsrate zieht.
|
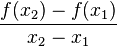stellt den Differenzenquotienten dar. Der Differenzenquotient gibt die durchschnittliche Änderungsrate von f über dem Intervall [
;
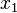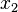] an.
|
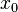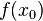) und Q(
).
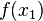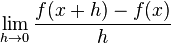heißt Differenzialquotient. Dieser Quotient ist der Grenzwert des Differenzenquotienten. Er gibt die Steigung der Tangente an der Stelle x an und entspricht der Ableitung an dieser Stelle.| Aufgabe 3: Änderungsraten im Sachzusammenhang
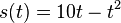a) Berechne den zurückgelegten Weg nach 3 und 5 Sekunden. b) Berechne die Geschwindigkeit, die Tim nach 3 Sekunden bzw. nach 5 Sekunden mit seinem Fahrrad erreicht hat. c) Warum hat die oben genannte Formel im vorliegenden Sachzusammenhang für
|
für ![t\in [0;5]](/images/math/d/1/7/d17e4f93b0be76b84d0dd79694840cff.png)
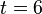keinen Sinn?
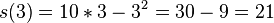. Nach 5 Sekunden hat er 25 Meter zurückgelegt, denn es gilt 
.
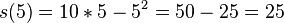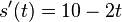entspricht der Geschwindigkeit. 
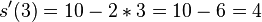und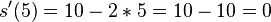 
.
