Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Übungen: Unterschied zwischen den Versionen
(Kategorie:Manipulationen an Funktionen) |
|||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 16: | Zeile 16: | ||
| gerade || Eine Funktion, die nur x-Potenzen mit geraden Exponenten enthält, nennt man ... Funktion. | | gerade || Eine Funktion, die nur x-Potenzen mit geraden Exponenten enthält, nennt man ... Funktion. | ||
|- | |- | ||
| − | | gleich || Ist eine Funktion achsensymmetrisch zur y-Achse, so sind die x-Werte ... weit vom Ursprung entfernt. | + | | gleich || Ist eine Funktion achsensymmetrisch zur y-Achse, so sind die Funktionswerte für betragsmäßig gleiche x-Werte ... weit vom Ursprung entfernt. |
|- | |- | ||
| − | | Spiegelpunkt || | + | | Spiegelpunkt || Bei der Punktspiegelung entsteht der ... aus dem ursprünglichen Punkt, indem die x- und y-Koordinate mit -1 multipliziert wird. |
|- | |- | ||
| − | | umgekehrtem || Liegt | + | | umgekehrtem || Liegt Punktsymmetrie zum Ursprung vor, hat die Funktion für x und -x betragsmäßig den gleichen Wert mit ... Vorzeichen. |
|- | |- | ||
| doppelt || Multipliziert man einen Funktionsterm mit 2, so ist der Funktionswert ... so weit von der x-Achse entfernt wie der ursprüngliche Funktionswert. | | doppelt || Multipliziert man einen Funktionsterm mit 2, so ist der Funktionswert ... so weit von der x-Achse entfernt wie der ursprüngliche Funktionswert. | ||
|- | |- | ||
| − | | halb || Die | + | | halb || Die Werte der Funktion g(x) = f (a ∙ x) sind für a = 2 genau ... so weit von der y-Achse entfernt wie die x-Werte von f. |
|- | |- | ||
| Asymptote || Die Gerade, der sich die Grenzwerte im Unendlichen annähern, heißt ... . | | Asymptote || Die Gerade, der sich die Grenzwerte im Unendlichen annähern, heißt ... . | ||
|- | |- | ||
| − | | Limes || Mit dem ... Symbol werden die Funktionswerte für immer größer oder kleiner werdende x-Werte untersucht. | + | | Limes || Mit dem ... -Symbol werden die Funktionswerte für immer größer oder kleiner werdende x-Werte untersucht. |
|- | |- | ||
| − | | Grenzwert || Wird ein Graph durch die Gerade y=5 begrenzt,so ist 5 der ... der Funktion. | + | | Grenzwert || Wird ein Graph durch die Gerade y = 5 begrenzt, so ist 5 der ... der Funktion. |
|- | |- | ||
| divergent || Nähert sich eine Funktion für immer größer werdende x-Werte keiner festen Grenze an, ist sie ... . | | divergent || Nähert sich eine Funktion für immer größer werdende x-Werte keiner festen Grenze an, ist sie ... . | ||
| Zeile 63: | Zeile 63: | ||
<center><div class="lueckentext-quiz">Definition: | <center><div class="lueckentext-quiz">Definition: | ||
Nähert sich der Graph einer Funktion f für '''immer größer werdende''' x-Werte einer '''Zahl''' G immer weiter an, so nennt man G den '''Grenzwert''' für x gegen +∞:<br /> | Nähert sich der Graph einer Funktion f für '''immer größer werdende''' x-Werte einer '''Zahl''' G immer weiter an, so nennt man G den '''Grenzwert''' für x gegen +∞:<br /> | ||
| − | In mathematischer Schreibweise:<math>\lim_{x\rightarrow\infty} f(x) = G </math><br /> Auf gleiche Weise definiert man den Grenzwert einer Funktion f für '''immer kleiner werdende''' x-Werte, also für x gegen -∞, mit <math> \lim_{x\rightarrow\ -\infty} f(x) | + | In mathematischer Schreibweise:<math>\lim_{x\rightarrow\infty} f(x) = G </math>.<br /> |
| − | </math> | + | |
| + | Auf gleiche Weise definiert man den Grenzwert einer Funktion f für '''immer kleiner werdende''' x-Werte, also für x gegen -∞, mit <math> \lim_{x\rightarrow\ -\infty} f(x)</math>.<br /> | ||
| + | |||
Nähert sich eine Funktion f für immer größere x-Werte '''keiner festen Grenze''' an, sondern fällt beispielsweise gegen '''-∞''',so heißt f divergent. <math>\lim_{x\rightarrow\ +\infty} f(x) = -\infty </math> | Nähert sich eine Funktion f für immer größere x-Werte '''keiner festen Grenze''' an, sondern fällt beispielsweise gegen '''-∞''',so heißt f divergent. <math>\lim_{x\rightarrow\ +\infty} f(x) = -\infty </math> | ||
</div></center> | </div></center> | ||
| Zeile 82: | Zeile 84: | ||
<div class="zuordnungs-quiz"> | <div class="zuordnungs-quiz"> | ||
{| | {| | ||
| − | | Punktsymmetrisch || sin(2x)|| x<sup>9</sup>-x || -3x<sup>299</sup>-x<sup>7</sup>+2x<sup>3</sup> || -x<sup>13</sup>+0 | + | | Punktsymmetrisch || sin (2x)|| x<sup>9</sup> - x || -3x<sup>299</sup> - x<sup>7</sup> + 2x<sup>3</sup> || -x<sup>13</sup> + 0,5x<sup>3</sup> |
|- | |- | ||
| − | | Achsensymmetrisch || 0,5z<sup>2</sup>-2 || x<sup>-12</sup>-3x<sup>-8</sup>|| -2x<sup>-4</sup>+3x<sup>2</sup>-1 || -0 | + | | Achsensymmetrisch || 0,5z<sup>2</sup> - 2 || x<sup>-12</sup> - 3x<sup>-8</sup>|| -2x<sup>-4</sup> + 3x<sup>2</sup> - 1 || -0,5x<sup>6</sup> + 4x<sup>4</sup> - 13 |
|- | |- | ||
| − | | Weder noch || x<sup>-5</sup>-x+3 || -2 | + | | Weder noch || x<sup>-5</sup> - x + 3 || -2,7x<sup>81</sup> - 6 || x<sup>42</sup> + x<sup>12</sup> - 6x || 3x<sup>3</sup> - x + 1 |
|- | |- | ||
|} | |} | ||
| Zeile 92: | Zeile 94: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | |||
'''Lückentext''' | '''Lückentext''' | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | Symmetrie: Bei der '''Achsensymmetrie''' gilt: f(x)= f(-x). Bei der Achsensymmetrie dürfen im Funktionsterm nur x- Potenzen mit ''' geraden''' Exponenten auftreten. | + | <u>Symmetrie:</u> <br /> |
| − | Bei der '''Punktsymmetrie''' gilt: f(-x)= -f(x). Bei der Punktsymmetrie dürfen im Funktionstern nur x- Potenzen mit ''' ungeraden''' Exponenten auftreten. | + | Bei der '''Achsensymmetrie''' gilt: f(x)= f(-x).<br /> |
| − | <br /> | + | Bei der Achsensymmetrie dürfen im Funktionsterm nur x- Potenzen mit ''' geraden''' Exponenten auftreten.<br /> |
| − | Verschiebung: Beim | + | |
| + | Bei der '''Punktsymmetrie''' gilt: f(-x)= -f(x).<br /> | ||
| + | Bei der Punktsymmetrie dürfen im Funktionstern nur x- Potenzen mit ''' ungeraden''' Exponenten auftreten.<br /> | ||
| + | |||
| + | <u>Verschiebung:</u> <br /> | ||
| + | Beim Term f(x)= g(x-a)+b entsteht der Graph von f aus dem Graphen von g, der für a<0 nach '''links''' und für a>0 nach '''rechts''' verschoben wird.<br /> | ||
| + | Der Parameter b<0 sorgt für die Verschiebung nach ''' unten''' und b>0 nach '''oben'''. | ||
</div> | </div> | ||
| Zeile 119: | Zeile 128: | ||
(von links oben nach rechts oben) | (von links oben nach rechts oben) | ||
(!von links oben nach rechts unten) | (!von links oben nach rechts unten) | ||
| − | |||
| − | |||
| − | |||
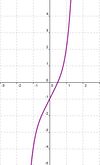
Welche Symmetrie besitzt die Funktion f(x)= x<sup>3</sup>? | Welche Symmetrie besitzt die Funktion f(x)= x<sup>3</sup>? | ||
| Zeile 127: | Zeile 133: | ||
Was ist die Voraussetzung für eine achsensymmetrische Funktion? | Was ist die Voraussetzung für eine achsensymmetrische Funktion? | ||
| − | (!Verlauf durch den Ursprung) (Alle Exponenten gerade) (!Alle Exponenten ungerade) (Größter Exponent ist gerade) | + | (!Verlauf durch den Ursprung) (Alle Exponenten gerade) (!Alle Exponenten ungerade) (!Größter Exponent ist gerade) |
Wie beeinflusst der Faktor t=2 die Parabel der Funktion f(x)= tx<sup>2</sup>+5? | Wie beeinflusst der Faktor t=2 die Parabel der Funktion f(x)= tx<sup>2</sup>+5? | ||
(!Sie wird +2 nach oben verschoben) (Sie wird enger) (!Sie wird weiter) (!Sie wird -2 nach unten verschoben) | (!Sie wird +2 nach oben verschoben) (Sie wird enger) (!Sie wird weiter) (!Sie wird -2 nach unten verschoben) | ||
| − | Wie heißt der Term der Funktion f(x)=x<sup>8</sup>-3 , wenn sie an der x-Achse gespiegelt wird? | + | Wie heißt der Term der Funktion f(x)=x<sup>8</sup>-3, wenn sie an der x-Achse gespiegelt wird? |
| − | (-x<sup>8</sup>-3) (!x<sup>8</sup>+3) ( | + | (!-x<sup>8</sup>-3) (!x<sup>8</sup>+3) (-x<sup>8</sup>+3) (!x<sup>-8</sup>-3) |
</div> | </div> | ||
| Zeile 150: | Zeile 156: | ||
<div class="memo-quiz" > | <div class="memo-quiz" > | ||
| − | + | Welche Verschiebung liegt hier vor?<br /> | |
| − | {| | + | Ordne die Verschiebung der passenden Funktionsgleichung zu. <br /> |
| − | | a(x)= (x+ | + | |
| + | {| | ||
| + | | a(x) = (x+4)<sup>2</sup>|| Verschiebung um 4 nach links | ||
|- | |- | ||
| − | | b(x)= x<sup>3</sup>- | + | | b(x) = x<sup>3</sup> - ½|| Verschiebung um ½ nach unten |
|- | |- | ||
| − | | c(x)= (x-4)<sup>4</sup>+11 || Verschiebung um 4 nach rechts und um 11 nach oben | + | | c(x) = (x-4)<sup>4</sup> + 11 || Verschiebung um 4 nach rechts und um 11 nach oben |
|- | |- | ||
| − | | d(x)= (x- | + | | d(x) = (x-4)<sup>13</sup> || Verschiebung um 4 nach rechts |
|- | |- | ||
| − | | e(x)= -x<sup>9</sup> || keine Verschiebung | + | | e(x) = -x<sup>9</sup> || keine Verschiebung |
|- | |- | ||
| − | | f(x)= -x<sup>6</sup>+ | + | | f(x) = -x<sup>6</sup> + ½ || Verschiebung um ½ nach oben |
|} | |} | ||
</div> | </div> | ||
| Zeile 237: | Zeile 245: | ||
'''Kreuzworträtsel zu Manipulationen an Funktionen'''<br /> | '''Kreuzworträtsel zu Manipulationen an Funktionen'''<br /> | ||
<br /> | <br /> | ||
| − | y-Richtung wird geschrieben als: | + | <u>Hinweis:</u> <br /> |
| − | Mehrere Worte werden zusammen geschrieben | + | y-Richtung wird geschrieben als: yRichtung <br /> |
| + | Mehrere Worte werden zusammen geschrieben. | ||
| Zeile 244: | Zeile 253: | ||
{| | {| | ||
|- | |- | ||
| − | | links|| Wie verschiebt sich der Graph, | + | | links|| Wie verschiebt sich der Graph von f(x + a) + b, für a größer 0? |
|- | |- | ||
| − | | Parameter|| | + | | Parameter|| Wie nennt man die veränderlichen Buchstaben in einer Funktionsgleichung? |
|- | |- | ||
| − | | rechts|| Wie verschiebt sich der Graph, wenn gilt: a kleiner 0? | + | | rechts|| Wie verschiebt sich der Graph von f(x + a) + b, wenn gilt: a kleiner 0? |
|- | |- | ||
| − | | | + | | xRichtung|| In welche Richtung wird der Graph der Funktion f(a ∙ x) gestreckt? |
|- | |- | ||
| − | | Spiegelung an der x-Achse|| Was passiert, wenn | + | | Spiegelung an der x-Achse|| Was passiert mit einem Graphen, wenn alle Funktionswerte mit -1 multipliziert werden? |
|- | |- | ||
| − | | | + | | yRichtung|| In welche Richtung wird der Graph von g gestreckt, wenn gilt: g = 2 ∙ f? |
|- | |- | ||
| Punktsymmetrie|| Auf was kann man schließen, wenn gleichweit vom Ursprung entfernte x-Werte immer den betragsgleichen Funktionswert mit unterschiedlichen Vorzeichen besitzen? | | Punktsymmetrie|| Auf was kann man schließen, wenn gleichweit vom Ursprung entfernte x-Werte immer den betragsgleichen Funktionswert mit unterschiedlichen Vorzeichen besitzen? | ||
| Zeile 260: | Zeile 269: | ||
| ungerade Funktion|| Wie nennt man eine Funktion mit nur ungeraden Exponenten? | | ungerade Funktion|| Wie nennt man eine Funktion mit nur ungeraden Exponenten? | ||
|- | |- | ||
| − | | Achsensymmetrie|| Welche Symmetrie liegt | + | | Achsensymmetrie|| Welche Symmetrie liegt vor, wenn eine Funktion f für gleich weit vom Ursprung entfernte x-Werte immer die gleichen Funktionswerte besitzt? |
|- | |- | ||
| − | + | | gerade Funktion|| Eine Funktionen mit nur geraden Exponenten nennt man ...? | |
| − | + | ||
| − | | gerade Funktion|| Funktionen mit nur geraden Exponenten nennt man... | + | |
|- | |- | ||
| lim|| Mit welchem Kürzel untersucht man die Funktionswerte für immer größer oder kleiner werdende x-Werte? | | lim|| Mit welchem Kürzel untersucht man die Funktionswerte für immer größer oder kleiner werdende x-Werte? | ||
|- | |- | ||
| − | | Limes|| Wofür steht 'lim | + | | Limes|| Wofür steht die Abkürzung 'lim'? |
| − | + | ||
| − | + | ||
|} | |} | ||
</div> | </div> | ||
| Zeile 290: | Zeile 295: | ||
'''1. Symmetrie''' | '''1. Symmetrie''' | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | Alle Exponenten, die in einem Funktionsterm auftauchen müssen '''gerade sein''', um Achsensymmetrie zur y-Achse | + | Alle Exponenten, die in einem Funktionsterm auftauchen, müssen '''gerade sein''', um Achsensymmetrie zur y-Achse nachweisen zu können.<br /> |
| + | Wenn der Funktionsterm einer '''geraden Funktion''' vorliegt, kann man darauf schließen, dass alle gleich weit '''vom Ursprung entfernten''' x-Werte '''gleiche Funktionswerte''' haben.<br /> | ||
| + | Daraus folgt: f(x)= f(-x).<br /> | ||
| + | |||
| + | Eine Funktion f(x), die nur ungerade Exponenten besitzt, ist '''punktsymmetrisch zum Ursprung'''. <br /> | ||
| + | Die '''Punktsymmetrie zum Ursprung''' zeigt sich am Graphen dadurch, dass alle '''Funktionswerte''', die gleich weit vom Ursprung entfernt sind, '''betragsmäßig''' gleich sind, aber unterschiedliche '''Vorzeichen''' haben.<br /> | ||
| + | Daraus folgt: f(-x)= -f(x) | ||
</div> | </div> | ||
| Zeile 298: | Zeile 309: | ||
'''2. Verschiebung''' | '''2. Verschiebung''' | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | + | Der Graph einer Funktion f(x - a) + b wird um a Einheiten in '''x-Richtung''' bzw. um b Einheiten in '''y-Richtung''' verschoben.<br /> | |
| + | Ist a>0 wird der Graph nach '''rechts''' verschoben, bei a<0 nach '''links'''. <br /> | ||
| + | Für b>0 wird der Graph in '''positive Richtung''', bei b<0 in '''negative Richtung''' verschoben. <br /> | ||
| + | Folglich sorgt a unabhängig von b für eine '''Verschiebung entlang der x-Achse''', bzw. b unabhängig von a für eine '''Verschiebung entlang der y-Achse'''. <br /> | ||
</div> | </div> | ||
| Zeile 306: | Zeile 320: | ||
'''3. Streckung und Spiegelung''' | '''3. Streckung und Spiegelung''' | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | Bei einer Funktion der Form g(x)= -a⋅f(x) handelt es sich bei | + | Bei einer Funktion der Form g(x) = -a ⋅ f(x) handelt es sich bei '''a''' um den Streckungsfaktor, der den Graphen in '''y-Richtung''' streckt. <br /> |
| − | Bei einer Funktion der Form g(x)=f(-a⋅x) beträgt der Streckungsfaktor stets '''1/a''', der die Funktion in '''x-Richtung''' streckt. Durch das negative Vorzeichen in der Klammer wird der Graph an der '''y-Achse''' gespiegelt. | + | Zudem wird der Graph durch das negative Vorzeichen an der '''x-Achse''' gespiegelt.<br /> |
| + | |||
| + | Bei einer Funktion der Form g(x) = f(-a ⋅ x) beträgt der Streckungsfaktor stets '''1/a''', der die Funktion in '''x-Richtung''' streckt. <br /> | ||
| + | Durch das negative Vorzeichen in der Klammer wird der Graph an der '''y-Achse''' gespiegelt. | ||
</div> | </div> | ||
| Zeile 315: | Zeile 332: | ||
'''4. Grenzwerte im Unendlichen''' | '''4. Grenzwerte im Unendlichen''' | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | Kommt der Graph einer Funktion f(x) einer Zahl G immer näher, so ist G der '''Grenzwert''' der Funktion f für x <math>\rightarrow\</math>+<math>\infty</math>. <br />Der Grenzwert einer Funktion f(x) für '''immer kleiner werdende x-Werte''' beträgt <math>\lim_{x\rightarrow-\infty} f(x)</math>, gesprochen: "Limes von f(x) für x gegen -<math>\infty</math>". <br />Die '''waagrechte Asymptote''' für den Graphen der Funktion f ergibt sich aus der Gerade '''y=G'''. f heißt '''divergent''' wenn sich die Funktion f(x) für immer größer werdende x-Werte keiner festen Grenze annähert, sondern | + | Kommt der Graph einer Funktion f(x) einer Zahl G immer näher, so ist G der '''Grenzwert''' der Funktion f für x <math>\rightarrow\</math>+<math>\infty</math>. <br /> |
| + | Der Grenzwert einer Funktion f(x) für '''immer kleiner werdende x-Werte''' beträgt <math>\lim_{x\rightarrow-\infty} f(x)</math>, gesprochen:<br /> | ||
| + | "Limes von f(x) für x gegen - <math>\infty</math>". <br /> | ||
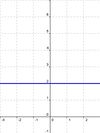
| + | Die '''waagrechte Asymptote''' für den Graphen der Funktion f ergibt sich aus der Gerade '''y = G'''. <br /> | ||
| + | |||
| + | f heißt '''divergent''' wenn sich die Funktion f(x) für '''immer größer werdende x-Werte''' keiner festen Grenze annähert, sondern bspw. gegen -<math>\infty</math> fällt.<br /> | ||
| + | Man schreibt: <math>\lim_{x\rightarrow\infty} f(x)</math>= -<math>\infty</math>. | ||
</div> | </div> | ||
| Zeile 331: | Zeile 354: | ||
}} | }} | ||
|} | |} | ||
| + | |||
| + | |||
| + | {{SORTIERUNG:{{SUBPAGENAME}}}} | ||
| + | [[Kategorie:Manipulationen an Funktionen]] | ||
Aktuelle Version vom 2. Mai 2018, 20:31 Uhr
|
Gruppe 1
|
|
Gruppe 2
Definition:
Nähert sich der Graph einer Funktion f für immer größer werdende x-Werte einer Zahl G immer weiter an, so nennt man G den Grenzwert für x gegen +∞: Auf gleiche Weise definiert man den Grenzwert einer Funktion f für immer kleiner werdende x-Werte, also für x gegen -∞, mit Nähert sich eine Funktion f für immer größere x-Werte keiner festen Grenze an, sondern fällt beispielsweise gegen -∞,so heißt f divergent.
|
|
Gruppe 3 Zuordnugsquiz zur Symmetrie von Funktionen
Lückentext Symmetrie: Bei der Punktsymmetrie gilt: f(-x)= -f(x). Verschiebung:
|
|
Gruppe 4 Wie verläuft die Funktion f(x)= 2x3+x4+7? (!von links unten nach rechts oben) (!von links unten nach rechts unten) (von links oben nach rechts oben) (!von links oben nach rechts unten) Welche Symmetrie besitzt die Funktion f(x)= x3? (!Achsensymmetrie zur y-Achse) (Punktsymmetrie zum Ursprung) (!Keine Symmetrie) Was ist die Voraussetzung für eine achsensymmetrische Funktion? (!Verlauf durch den Ursprung) (Alle Exponenten gerade) (!Alle Exponenten ungerade) (!Größter Exponent ist gerade) Wie beeinflusst der Faktor t=2 die Parabel der Funktion f(x)= tx2+5? (!Sie wird +2 nach oben verschoben) (Sie wird enger) (!Sie wird weiter) (!Sie wird -2 nach unten verschoben) Wie heißt der Term der Funktion f(x)=x8-3, wenn sie an der x-Achse gespiegelt wird? (!-x8-3) (!x8+3) (-x8+3) (!x-8-3)
|
|
Gruppe 5 Memory zu VerschiebungenWelche Verschiebung liegt hier vor?
|
|
Gruppe 7 Kreuzworträtsel zu Manipulationen an Funktionen
|
|
Gruppe 8 Lückentext-Quiz zum Thema "Manipulationen an Funktionen"
Alle Exponenten, die in einem Funktionsterm auftauchen, müssen gerade sein, um Achsensymmetrie zur y-Achse nachweisen zu können. Eine Funktion f(x), die nur ungerade Exponenten besitzt, ist punktsymmetrisch zum Ursprung.
Der Graph einer Funktion f(x - a) + b wird um a Einheiten in x-Richtung bzw. um b Einheiten in y-Richtung verschoben.
Bei einer Funktion der Form g(x) = -a ⋅ f(x) handelt es sich bei a um den Streckungsfaktor, der den Graphen in y-Richtung streckt. Bei einer Funktion der Form g(x) = f(-a ⋅ x) beträgt der Streckungsfaktor stets 1/a, der die Funktion in x-Richtung streckt.
Kommt der Graph einer Funktion f(x) einer Zahl G immer näher, so ist G der Grenzwert der Funktion f für x Fehler beim Parsen(Lexikalischer Fehler): \rightarrow\
+ f heißt divergent wenn sich die Funktion f(x) für immer größer werdende x-Werte keiner festen Grenze annähert, sondern bspw. gegen -
|
| Zurück zur Übersicht |
Manipulationen an Funktionen
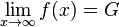 .
.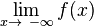 .
.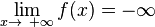
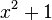
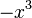
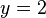
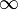 .
. 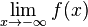 , gesprochen:
, gesprochen: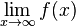 = -
= -
