Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Rechenvorteile: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| (7 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
== <colorize>Rechenvorteile</colorize> == | == <colorize>Rechenvorteile</colorize> == | ||
| − | Die bereits bekannten Rechenvorteile gelten ebenso bei den rationalen Zahlen | + | |
| + | Die bereits bekannten Rechenvorteile gelten ebenso bei den rationalen Zahlen: | ||
'''<span style="color: #FF0000">1) Kommutativgesetz</span>''' | '''<span style="color: #FF0000">1) Kommutativgesetz</span>''' | ||
'''Beachte:''' | '''Beachte:''' | ||
| − | Du musst die Vorzeichen der Zahlen immer mitnehmen! | + | Summanden und Faktoren darfst du vertauschen.<br /> |
| + | Aber: Du musst die Vorzeichen der Zahlen dabei immer mitnehmen! | ||
[[Datei:Kommutativgesetz.PNG|Kommutativgesetz]] | [[Datei:Kommutativgesetz.PNG|Kommutativgesetz]] | ||
| Zeile 20: | Zeile 22: | ||
'''Beachte:''' | '''Beachte:''' | ||
| − | + | In Summen und Produkten darfst du Klammern setzen und verändern. <br /> | |
| + | Aber: Berechne Klammern immer zuerst! | ||
[[Datei:Assoziativgesetz.PNG|Assoziativgesetz]] | [[Datei:Assoziativgesetz.PNG|Assoziativgesetz]] | ||
| Zeile 28: | Zeile 31: | ||
'''Beachte:''' | '''Beachte:''' | ||
| − | Punkt vor Strich! | + | Du darfst gemeinsame Faktoren ausklammern.<br /> |
| + | Aber: Beachte die Regel "Punkt vor Strich"! | ||
[[Datei:Distributivgesetz.PNG|Distributivgesetz]] | [[Datei:Distributivgesetz.PNG|Distributivgesetz]] | ||
| Zeile 36: | Zeile 40: | ||
<small><colorize>Verbindung der Grundrechenarten</colorize></small> | <small><colorize>Verbindung der Grundrechenarten</colorize></small> | ||
| − | |||
| − | + | Hier hast du ein Beispiel anhand dieses Terms: | |
| + | <big>(</big><math>\frac{16}{10}</math><big> + 4,5) : </big><math>\frac{2}{5}</math><big> + (2·10−2,25)</big> | ||
| − | |||
| + | '''''<span style="color: #FF0000">Schritt 1:</span>''''' <math>\frac{16}{10}</math><big> + 4,5 = </big><math>\frac{16}{10}</math> <big>+</big> <math>\frac{45}{10}</math><big> = </big> <math>\frac{61}{10}</math> = <big> 6,1</big> | ||
| − | |||
| − | '''''<span style="color: #FF0000">Schritt | + | '''''<span style="color: #FF0000">Schritt 2:</span>''''' <big> (2·10−2,25)</big> = <big>(20−2,25)</big> = <big> 17,75</big> |
| − | |||
| + | '''''<span style="color: #FF0000">Schritt 3:</span>''''' <math>\frac{2}{5}</math> <big>= 0,4</big> | ||
| + | |||
| + | |||
| + | |||
| + | '''''<span style="color: #FF0000">Schritt 4:</span>''''' <big> (6,1 : 0,4) + 17,75 = 33 </big> | ||
| + | |||
| + | <br /> | ||
| + | <br /> | ||
<popup name= Aufgaben> | <popup name= Aufgaben> | ||
| Zeile 57: | Zeile 67: | ||
Aufgabe 1 | Aufgabe 1 | ||
<iframe src="https://learningapps.org/watch?v=p7pp4vtnv18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=p7pp4vtnv18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | <br /> | ||
| + | |||
| + | Aufgabe 2: Berechne die Aufgaben und klicke die richtige Lösung an. Tipp: Nehme ein Notizblatt zur Hilfe | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | |||
| + | <math>\frac{2}{5}</math><big> - </big><math>\frac{6}{4}</math><big> · </big><math>\frac{1}{3}</math><big> + 0,1 =</big> | ||
| + | (!<math>\frac{2}{5}</math>) (0) (!<math>\frac{2}{3}</math>) (!1) (!<math>\frac{1}{5}</math>) | ||
| + | |||
| + | </div> | ||
| + | <br /> | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | |||
| + | <math>\frac{6}{15}</math><big> · </big><math>\frac{3}{8}</math><big> + 1 = </big> | ||
| + | (!<math>\frac{21}{20}</math>) (<math>\frac{23}{20}</math>) (!<math>\frac{19}{20}</math>) (!<math>\frac{12}{20}</math>) (!<math>\frac{25}{20}</math>) | ||
| + | |||
| + | </div> | ||
| + | <br /> | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | |||
| + | <big>- 1 · [ 5 ·(</big> <math>\frac{1}{4}</math><big> + </big><math>\frac{1}{3}</math><big>)] + </big><math>\frac{3}{4}</math> | ||
| + | (!<math>\frac{1}{2}</math>) (!<math>\frac{13}{6}</math>) (!<math>\frac{7}{12}</math>) (<big> - </big><math>\frac{13}{6}</math>) (!<math>\frac{5}{8}</math>) | ||
| + | |||
| + | </div> | ||
| + | |||
| + | </popup> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | |||
| + | {{Vorlage:Lesepfad Ende | ||
| + | |Link zurück=[[Julius-Echter-Gymnasium/Mathematik/Rechnen mit rationalen Zahlen|zum Rechnen mit rationalen Zahlen]] | ||
| + | |Link vor=[[Julius-Echter-Gymnasium/Mathematik/Berechnung von Grundwert, Prozentsatz und Prozentwert|zur Berechnung von Grundwert, Prozentsatz und Prozentwert]] | ||
| + | |Text Copyright= | ||
| + | }} | ||
Aktuelle Version vom 29. Januar 2020, 09:05 Uhr
Rechenvorteile
Die bereits bekannten Rechenvorteile gelten ebenso bei den rationalen Zahlen:
1) Kommutativgesetz
Beachte: Summanden und Faktoren darfst du vertauschen.
Aber: Du musst die Vorzeichen der Zahlen dabei immer mitnehmen!
2) Assoziativgesetz
Beachte: In Summen und Produkten darfst du Klammern setzen und verändern.
Aber: Berechne Klammern immer zuerst!
3) Distributivgesetz
Beachte: Du darfst gemeinsame Faktoren ausklammern.
Aber: Beachte die Regel "Punkt vor Strich"!
Verbindung der Grundrechenarten
Hier hast du ein Beispiel anhand dieses Terms:
(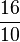 + 4,5) :
+ 4,5) :  + (2·10−2,25)
+ (2·10−2,25)
Schritt 1: 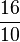 + 4,5 =
+ 4,5 = 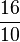 +
+ 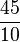 =
= 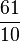 = 6,1
= 6,1
Schritt 2: (2·10−2,25) = (20−2,25) = 17,75
Schritt 3:  = 0,4
= 0,4
Schritt 4: (6,1 : 0,4) + 17,75 = 33
| zum Rechnen mit rationalen Zahlen | zur Berechnung von Grundwert, Prozentsatz und Prozentwert |
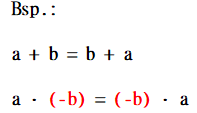
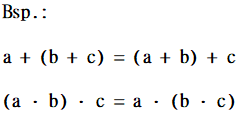
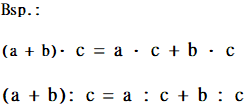
 ·
·  + 0,1 =
(!
+ 0,1 =
(! ) (!1) (!
) (!1) (! )
)
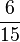 ·
·  + 1 =
(!
+ 1 =
(!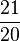 ) (
) (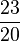 ) (!
) (!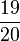 ) (!
) (!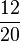 ) (!
) (!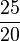 )
)
 +
+  (!
(! ) (!
) (!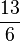 ) (!
) (!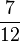 ) ( -
) ( -  )
)

