Achtung:

Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.

Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.

Gerne kannst Du natürlich weiterarbeiten

im neuen Projektwiki (projekte.zum.de).

Trigonometrische Funktionen: Unterschied zwischen den Versionen

Aus Projektwiki - ein Wiki mit Schülern für Schüler.
Wechseln zu: Navigation, Suche
Zeile 32: Zeile 32:
 
(!b < 0)  (d > 0) (!a < 1) (!c > 1) (!d < 1) (!b > 1)
 
(!b < 0)  (d > 0) (!a < 1) (!c > 1) (!d < 1) (!b > 1)
  
−
Welcher Parameter sorgt für eine Verschiebung in negative y- Richtung?
+
Welcher Parameter sorgt für eine Verschiebung in negative x- Richtung?
 
(!a < 1) (c < 0) (!d > 1) (!a = 1) (!b > 1) (!c > 0)  
 
(!a < 1) (c < 0) (!d > 1) (!a = 1) (!b > 1) (!c > 0)  
  
 
Mit welcher Parametereinstellung werden die Graphen an der x- Achse gespiegelt?
 
Mit welcher Parametereinstellung werden die Graphen an der x- Achse gespiegelt?
−
(a = -1) (!b = 0) (!c = -1) (!d = 0)  
+
(a = -1) (!b = 0) (!c = -1) (!d = 0) (c = <math>\prod_{}</math>) (c = - <math>\prod_{}</math>)
  
 
Welcher Parameter streckt die Graphen in x- Richtung?
 
Welcher Parameter streckt die Graphen in x- Richtung?
Zeile 59: Zeile 59:
 
| width = "20%"|
 
| width = "20%"|
 
|
 
|
−
*cos(0,2 ∙ x)
+
*0,5 ∙ cos(x)
−
*0,5 ∙ cos(0,2 ∙ x)
+
*0,5 ∙ cos(x) -2
 
*0,5 ∙ cos(0,2 ∙ x) - 2
 
*0,5 ∙ cos(0,2 ∙ x) - 2
 
*0,5 ∙ cos(0,2 ∙ x + 1,5) - 2
 
*0,5 ∙ cos(0,2 ∙ x + 1,5) - 2

Version vom 29. Juni 2013, 13:14 Uhr


Wiederhole an diesem GeoGebra-Applet dein Wissen über
die allgemeine Sinusfunkion f (x) = a ∙ sin(b ∙ x - c) + d und
die allgemeine Cosinusfunktion g (x) = a ∙ cos(b ∙ x - c) + d.

Über die vier Schieberegler a, b, c, d wird der Funktionsterm und damit auch der Graph der beiden Funktionen verändert.
Du kannst die beiden Funktionen auch einzeln betrachten, indem du eine von ihnen über das Kontrollkästchen verbirgst.


Übung

1. Multiple Choice

Welcher Parameter verschiebt die ursprünglichen Graphen nach oben? (!b < 0) (d > 0) (!a < 1) (!c > 1) (!d < 1) (!b > 1)

Welcher Parameter sorgt für eine Verschiebung in negative x- Richtung? (!a < 1) (c < 0) (!d > 1) (!a = 1) (!b > 1) (!c > 0)

Mit welcher Parametereinstellung werden die Graphen an der x- Achse gespiegelt? (a = -1) (!b = 0) (!c = -1) (!d = 0) (c = \prod_{}) (c = - \prod_{})

Welcher Parameter streckt die Graphen in x- Richtung? (!a) (b) (!c) (!d)

Welcher Parameter streckt die Graphen in Richtung der y- Achse? (a) (!b) (!c) (!d)




2. Denksport

Überlege dir, wie die Graphen der folgenden Funktionen aussehen müssen und kontrolliere dich selbst, indem du im Applet die Schieberegler entsprechend einstellst:

  • sin(3 ∙ x)
  • sin(3 ∙ x - 2)
  • sin(3 ∙ x - 2) + 1
  • 2 ∙ sin(3 ∙ x - 2) + 1
  • 0,5 ∙ cos(x)
  • 0,5 ∙ cos(x) -2
  • 0,5 ∙ cos(0,2 ∙ x) - 2
  • 0,5 ∙ cos(0,2 ∙ x + 1,5) - 2


Zurück zum Strecken und Spiegeln von Funktionsgraphen Los geht´s mit der Streckung in y- Richtung

Manipulationen an Funktionen

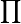Von „https://projektwiki.zum.de/index.php?title=Manipulationen_an_Funktionen/Strecken_und_Spiegeln_von_Funktionsgraphen/Trigonometrische_Funktionen&oldid=3090“