Streckung in y- Richtung

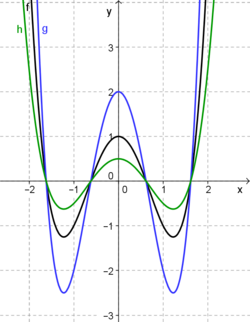
Fülle die Wertetabelle auf deinem Arbeitsblatt vollständig aus. x - 1,5 - 1 - 0,5 0 0,5 1 1,5 f(x) = x4 - 3x2 + 1 g(x) = 2 ∙ f(x) h(x) = ½ ∙ f(x) Ergänze den folgenden Lückentext, kontrolliere deine Antworten und übertrage die richtige Lösung auf dein Arbeitsblatt! Wie ändern sich die Funktionswerte von f (x) im Vergleich zu g(x), bzw. zu h(x)? Für g(x) = 2 ∙ f(x) erhält man jeden Funktionswert von g, indem man den entsprechenden Funktionswert von f mit 2 multipliziert. Die Funktionswerte von g sind dann immer doppelt so weit von der x- Achse entfernt, wie die Funktionswerte von f. Äquivalent ergibt sich jeder Funktionswert von h(x) = ½ ∙ f(x), indem man jeden Funktionswert von f mit ½ multipliziert. Die Funktionswerte von h sind damit immer halb so weit von der x- Achse entfernt, wie die Funktionswerte von f.

Allgemein Das folgende Applet zeigt die Funktion f (x) = x4 - 3x2 + 1. Durch den Schieberegler a lässt sich eine weitere Funktion g(x) = a ∙ f(x), für a > 1, bzw. eine Funktion h(x) = a ∙ f(x), für 0 < a < 1 anzeigen. Wie verändert sich g, bzw. h, wenn a größer oder kleiner wird? Achte dabei besonders auf die drei markierten Punkte. Die Veränderung lässt sich am besten an allen x- Werten beobachten, in denen f (x) = 1 ist. An diesen Stellen entspricht der Faktor a genau dem Funktionswert von g, bzw. h. Fülle die Lücken aus und vervollständige anschließend den MERKE-Kasten auf deinem Arbeitsblatt! MERKE: Für eine Funktion g(x) = a ∙ f(x) mit a > 1 sind die Funktionswerte von g immer a-mal so weit von der x- Achse entfernt, wie die Funktionswerte von f. Man spricht von einer Streckung des Graphen von g in y- Richtung mit dem Streckungsfaktor a.

Übung Hast du alles verstanden? Teste dein Wissen mit dieser Zuordnungsübung: Zurück zum Strecken und Spiegeln von Funktionsgraphen Weiter zur Streckung in x- Richtung Manipulationen an Funktionen