Streckung in x- Richtung

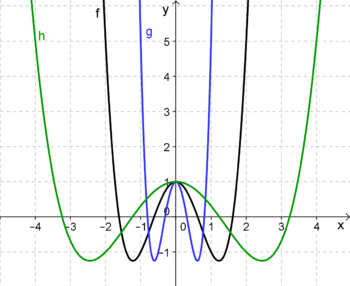
Im Bild siehst du drei Funktionen mit den folgenden Funktionstermen: f(x) = x4 - 3 x2 + 1, g(x) = f (2 ∙ x) = (2 ∙ x)4 - 3 (2 ∙ x)2 + 1 und h(x) = f (½ ∙ x) = (½ ∙ x)4 - 3 (½ ∙ x)2 + 1 Im Gegensatz zur Streckung in y- Richtung durch g(x) = a ∙ f (x) wird bei der Funktion g(x) = f (a ∙ x) der Parameter a mit jedem auftretenden x- Wert multipliziert. Damit muss auch die jeweilige Potenz auf den Parameter a angewendet werden. Mit den Potenzgesetzen folgt: g(x) = 24 ∙ x4 - 3 ∙ 22 ∙ x2 + 1 und h(x) = (½)4 ∙ x4 - 3 ∙ (½)2 ∙ x2 + 1. Fülle die Wertetabelle auf deinem Arbeitsblatt vollständig aus. Was fällt dir auf? x - 4 - 2 - 1 0 1 2 4 f(x) = x4 - 3x² + 1 g(x) = f (2 ∙ x) h(x) = f (½ ∙ x) Vermerke auch deine Beobachtungen, indem du den Lückentext ausfüllst, kontrollierst und dann auf das Arbeitsblatt überträgst. Für eine Funktion g(x) = f (2 ∙ x) sind alle Funktionswerte g(x) gleich den Funktionswerten f (2 ∙ x). Also sind die Funktionswerte f (x) an jeder Stelle x genau doppelt so weit von der y- Achse entfernt, wie die Funktionswerte g(x) für den gleichen x- Wert. Umgekehrt ist g(x) für jeden x- Wert genau halb so weit von der y- Achse entfernt, wie f(x) für den gleichen x- Wert.

Allgemein Gegeben ist die Funktion f: x -> x4 - 3x2 + 1, sowie zwei weitere Funktionen g(x) = f (a ∙ x), für a > 1, und h(x) = f (a ∙ x), für a < 1. Vergleiche die Schnittpunkte der drei Funktionen f, g und h mit den Koordinatenachsen. Was fällt dir auf, wenn du ihre Lage betrachtest? Setzte den Schieberegler a auf ganzzahlige Werte, um eine allgemeine Regel zu formulieren. Warum haben alle drei Graphen den gleichen Schnittpunkt mit der y- Achse? Lösung anzeigen Lösung verstecken Betrachte den Schnittpunkt Sf(1,62/0) von f mit der x- Achse. g2(x) = f (2∙ x) hat dann den Schnittpunkt Sg(0,81/0) mit der x- Achse. $\Rightarrow$ Die x- Koordinate von Sg ist genau halb so groß, wie die von Sf. Für g3(x) = f (3∙ x) liegt der Achsenschnittpunkt bei Sg(0,54/0). $\Rightarrow$ Hier ist die x- Koordinate von Sg ein Drittel so groß, wie die von Sf. Alle Graphen schneiden den Punkt (0/1), da alle Funktionsterme die Konstante + 1 enthalten. Übertrage die Lücken, nachdem du sie hier überprüft hast, auf dein Arbeitsblatt. MERKE: Die x- Werte einer Funktion g(x) = f (a ∙ x), für a > 0, sind immer $\frac{1}{a}$-mal so weit von der y- Achse entfernt, wie die x- Werte von f. Der Graph von g wird von der y- Achse aus in x- Richtung mit dem Streckungsfaktor $\frac{1}{a}$ gestreckt.

Übung Teste dich selbst, indem du den Funktionsgraphen ihre Gleichungen zuordnest. Zurück zur Streckung in y- Richtung Weiter zur Spiegelung an der x- Achse Manipulationen an Funktionen