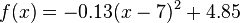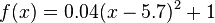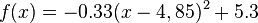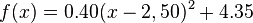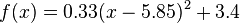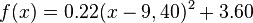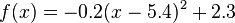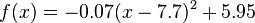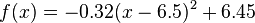Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Workshop Lernpfad
Inhaltsverzeichnis |
Spielwiese
Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben.
Ebenso sind andere Farben möglich, um etwas hervorzuheben.
Vorlagen
|
Inhalt |
|
Inhalt |
|
Inhalt |
30px Übung
Inhalt |
30px Merke
Merksatz |
Dateien
Interaktive Applets
Kombinationen
Quadratische Funktionen in Scheitelpunktform
(Inhalte aus dem Lernpfad Quadratische Funktionen erkunden)
30px Merke
Terme quadratischer Funktionen können in der Form |
|
Was passiert, wenn man statt der Funktion
a) Notiere Vermutungen darüber, wie die Graphen der Funktionen (1), (2) und (3) aussehen (ohne diese zu zeichnen!). b) Zeichne die drei Graphen in ein Koordinatensystem und überprüfe deine Vermutungen aus Aufgabenteil a). Welche deiner Vermutungen treffen zu? Welche kannst du mit Hilfe der Funktionsgraphen korrigieren? |
|
|
|
Finde Werte für a, d und e, so dass
|


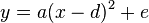 angegeben werden (wobei a ≠ 0). Diese Darstellungsform nennt man Scheitelpunktform, da sich direkt aus dem Term der Scheitelpunkt ablesen lässt. Er hat die Koordinaten
angegeben werden (wobei a ≠ 0). Diese Darstellungsform nennt man Scheitelpunktform, da sich direkt aus dem Term der Scheitelpunkt ablesen lässt. Er hat die Koordinaten 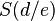 .
.
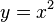 folgenden Funktionen gegeben hat:
folgenden Funktionen gegeben hat:
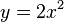 , (2)
, (2) 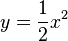 und (3)
und (3) 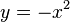 ?
?
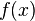 die Kurve auf dem Bild möglichst gut beschreibt. Entscheide dich für drei Hintergrundbilder deiner Wahl und notiere den Funktionsterm in deinem Hefter. Wenn du noch weiter arbeiten möchtest, kannst du auch einige der übrigen Hintergundbilder bearbeiten.
die Kurve auf dem Bild möglichst gut beschreibt. Entscheide dich für drei Hintergrundbilder deiner Wahl und notiere den Funktionsterm in deinem Hefter. Wenn du noch weiter arbeiten möchtest, kannst du auch einige der übrigen Hintergundbilder bearbeiten.