Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Benutzer:Tina WWU3: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | ==Über mich== | ||
| + | *Seminar: [[Digitale Werkzeuge in der Schule|Wikiprojekt zu dem Seminar "DiWerS]] | ||
| + | *Projekt: [[Digitale_Werkzeuge_in_der_Schule/Trainingsfeld_Ableitungen|Trainingsfeld Ableitungen]] | ||
| + | *betreut von: [[Benutzer:Elena Jedtke|Elena Jedtke]] | ||
| + | |||
| + | |||
{{Merke| | {{Merke| | ||
==Die lokale Änderungsrate== | ==Die lokale Änderungsrate== | ||
| − | < | + | |
| + | Die '''lokale Änderungsrate''' einer Funktion <math>f</math> gibt die Steigung in einem Punkt an. Anders gesagt, gibt die lokale Änderungsrate die Steigung der '''Tangente''' an der Stelle <math>x</math> an. Die Steigung der Tangente entspricht der '''Ableitung''' der Funktion <math>f</math>. Somit lässt sich die lokale Änderungsrate mit Hilfe der Ablteitung <math>f'(x)</math> berechnen. | ||
| + | Eine weitere Methode zur Bestimmung der lokalen Änderungsrate ist, den Grenzwert des Differenzenquotienten zu bilden. | ||
| + | |||
| + | Der Grenzwert '''<math>\overrightarrow{h \rightarrow0}\frac{f(x+h)-f(x)} {h}</math>''' heißt '''Differenzialquotient'''. | ||
| + | |||
| + | <iframe width="560" height="315" src="https://www.youtube.com/embed/6HDhATXNCGU" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe>.}} | ||
==Unterscheidung der Änderungsraten== | ==Unterscheidung der Änderungsraten== | ||
| Zeile 53: | Zeile 65: | ||
'''c)''' Warum hat die oben genannte Formel im vorliegenden Sachzusammenhang für <math>t=6</math> keinen Sinn? | '''c)''' Warum hat die oben genannte Formel im vorliegenden Sachzusammenhang für <math>t=6</math> keinen Sinn? | ||
| − | + | <iframe src="https://learningapps.org/watch?v=pq5ma4hmn18" style="border:0px;width:100%;height:300px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | |
| − | <iframe src="https://learningapps.org/watch?v= | + | |
<popup name="Lösung a)">Nach 3 Sekunden hat Tim einen Weg von 21 Metern zurückgelegt, denn <math>s(3)=10*3-3^2=30-9=21</math>. Nach 5 Sekunden hat er 25 Meter zurückgelegt, denn es gilt <math>s(5)=10*5-5^2=50-25=25</math>.</popup> | <popup name="Lösung a)">Nach 3 Sekunden hat Tim einen Weg von 21 Metern zurückgelegt, denn <math>s(3)=10*3-3^2=30-9=21</math>. Nach 5 Sekunden hat er 25 Meter zurückgelegt, denn es gilt <math>s(5)=10*5-5^2=50-25=25</math>.</popup> | ||
Aktuelle Version vom 12. Januar 2019, 23:51 Uhr
Inhaltsverzeichnis[Verbergen] |
Über mich
- Seminar: Wikiprojekt zu dem Seminar "DiWerS
- Projekt: Trainingsfeld Ableitungen
- betreut von: Elena Jedtke
 Merke
Die lokale ÄnderungsrateDie lokale Änderungsrate einer Funktion Der Grenzwert . |
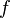gibt die Steigung in einem Punkt an. Anders gesagt, gibt die lokale Änderungsrate die Steigung der Tangente an der Stelle 
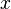an. Die Steigung der Tangente entspricht der Ableitung der Funktion 
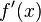berechnen.
Eine weitere Methode zur Bestimmung der lokalen Änderungsrate ist, den Grenzwert des Differenzenquotienten zu bilden.
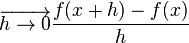heißt Differenzialquotient.
Unterscheidung der Änderungsraten
 Aufgabe 3: Unterscheidung der mittleren und lokalen Änderungsrate
a) Ordne die Karten jeweils richtig zu, indem ihr sie entweder zur mittleren oder lokalen Änderungsrate zieht.
|
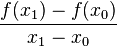stellt den Differenzenquotienten dar. Der Differenzenquotient gibt die mittlere Änderungsrate von f über dem Intervall [
;
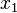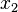] an.
|
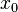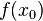) und Q(
).
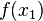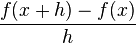heißt Differenzialquotient. Dieser Quotient ist der Grenzwert des Differenzenquotienten. Er gibt die Steigung der Tangente an der Stelle x an und entspricht der Ableitung an dieser Stelle.Änderungsraten im Sachzusammenhang
| Aufgabe 4: Änderungsraten im Sachzusammenhang
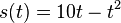a) Berechne den zurückgelegten Weg nach 3 und 5 Sekunden. b) Berechne die Geschwindigkeit, die Tim nach 3 Sekunden bzw. nach 5 Sekunden mit seinem Fahrrad erreicht hat. c) Warum hat die oben genannte Formel im vorliegenden Sachzusammenhang für
|
für ![t\in [0;5]](/images/math/d/1/7/d17e4f93b0be76b84d0dd79694840cff.png)
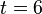keinen Sinn?
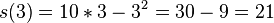. Nach 5 Sekunden hat er 25 Meter zurückgelegt, denn es gilt 
.
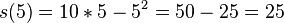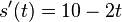entspricht der Geschwindigkeit. 
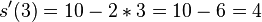und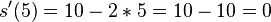 
.
