Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Zufallsexperimente: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 15: | Zeile 15: | ||
<u>Beispiel:</u> | <u>Beispiel:</u> | ||
| − | Fast jeder wird im Alltag regelmäßig Ausführer eines Zufallsexperiments. Ein gutes Beispiel sieht man beim Spielen von "Mensch ärger dich nicht". Wenn ein Spieler an der Reihe ist, würfelt er, um mit seiner Figur vorrücken zu können. Dieses Würfeln ist ein Zufallsexperiment. Wie wir in der Definition gelernt haben, ist | + | Fast jeder wird im Alltag regelmäßig Ausführer eines Zufallsexperiments. Ein gutes Beispiel sieht man beim Spielen von "Mensch ärger dich nicht". Wenn ein Spieler an der Reihe ist, würfelt er, um mit seiner Figur vorrücken zu können. Dieses Würfeln ist ein Zufallsexperiment. Wie wir in der Definition gelernt haben, ist ein Merkmal von Zufallsexperimenten die Unbekanntheit der Ergebnisse. Dies trifft auch beim Würfeln zu, da der Spieler nicht wissen kann, welche Zahl er würfeln wird. Obwohl das Würfelergebnis noch unbekannt ist, besteht das zweite Merkmal eines Zufallsexperiments darin, dass alle möglichen Ergebnisse bekannt sind. So auch beim Würfeln: Da die Spieler wissen, dass ein Würfel 6 Seiten hat, wissen sie auch, dass die Ergebnisse 1,2,3,4,5 oder 6 möglich sind. Welches Ergebnis genau eintritt ist allerdings unbekannt. |
<div style="padding:110px;background:#FFFFFF;border:0px groove;"> | <div style="padding:110px;background:#FFFFFF;border:0px groove;"> | ||
| Zeile 49: | Zeile 49: | ||
'''Auf einem Tisch liegen 2 blaue, 3 rote und 5 gelbe Stifte. Ohne hinzuschauen, wird einer der Stifte genommen und geschaut, welche Farbe er hat. | '''Auf einem Tisch liegen 2 blaue, 3 rote und 5 gelbe Stifte. Ohne hinzuschauen, wird einer der Stifte genommen und geschaut, welche Farbe er hat. | ||
'''<br /> | '''<br /> | ||
| − | Es handelt sich um ein Zufallsexperiment. Alle Merkmale treffen zu: Man kennt alle möglichen Ergebnisse, da man weiß, welche Stifte auf dem Tisch liegen. Da man ohne hinzuschauen einen Stift zieht, weiß man allerdings wieder nicht welchen der Stifte genau man ziehen wird. Der Ausgang ist also unbekannt. | + | Es handelt sich um ein Zufallsexperiment. Alle Merkmale treffen zu: Man kennt alle möglichen Ergebnisse, da man weiß, welche Stifte auf dem Tisch liegen. Da man ohne hinzuschauen einen Stift zieht, weiß man allerdings wieder nicht, welchen der Stifte genau man ziehen wird. Der Ausgang ist also unbekannt. |
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | '''Der Lehrer benotet die Schulaufgaben der Schüler/innen | + | '''Der Lehrer benotet die Schulaufgaben der Schüler/innen. |
'''<br /> | '''<br /> | ||
Hierbei handelt es sich um kein Zufallsexperiment, da der Lehrer die Noten nach Leistung vergibt und sie nicht zufällig benotet. | Hierbei handelt es sich um kein Zufallsexperiment, da der Lehrer die Noten nach Leistung vergibt und sie nicht zufällig benotet. | ||
| Zeile 67: | Zeile 67: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | Die absolute Häufigkeit gibt an, wie oft ein bestimmtes Ergebnis bei mehrmaliger Wiederholung eines Zufallsexperiments eintritt.<br /> | + | Die '''absolute''' Häufigkeit gibt an, '''wie oft''' ein bestimmtes Ergebnis bei mehrmaliger Wiederholung eines Zufallsexperiments eintritt.<br /> |
| − | Die relative Häufigkeit gibt an, wie groß der Anteil der absoluten Häufigkeit/ des Ergebnisses an der Gesamtanzahl der Durchführung des Zufallsexperiments ist. | + | Die '''relative''' Häufigkeit gibt an, wie groß der '''Anteil''' der absoluten Häufigkeit/ des Ergebnisses an der Gesamtanzahl der Durchführung des Zufallsexperiments ist. |
<br /> | <br /> | ||
<br /> | <br /> | ||
| Zeile 144: | Zeile 144: | ||
|} | |} | ||
| − | Nett to know: '''Empirisches Gesetz der großen Zahlen:''' | + | Nett to know/Gut zu wissen: '''Empirisches Gesetz der großen Zahlen:''' |
<br /> | <br /> | ||
Nach einer großen Anzahl von Durchführungen eines Zufallsexperiments stabilisiert sich die relative Häufigkeit auf einen bestimmten Wert. Die relative Häufigkeit verändert sich also bei weiteren Durchführungen kaum. | Nach einer großen Anzahl von Durchführungen eines Zufallsexperiments stabilisiert sich die relative Häufigkeit auf einen bestimmten Wert. Die relative Häufigkeit verändert sich also bei weiteren Durchführungen kaum. | ||
| + | <br /> | ||
| + | <br /> | ||
| + | |||
| + | Hier kannst du das Auswerten von Zufallsexperimenten üben: | ||
| + | <br /> | ||
| + | <br /> | ||
| + | |||
<popup name=Aufgaben > | <popup name=Aufgaben > | ||
| Zeile 156: | Zeile 163: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
| − | |||
|Augenzahl | |Augenzahl | ||
<br /> | <br /> | ||
| Zeile 206: | Zeile 211: | ||
=14% | =14% | ||
|- | |- | ||
| − | |||
| − | |||
|} | |} | ||
</div> | </div> | ||
| + | <br /> | ||
| + | <br /> | ||
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ||
Fülle die Lücken des Textes mit den richtigen Zahlen. | Fülle die Lücken des Textes mit den richtigen Zahlen. | ||
| + | <br /> | ||
| + | <br /> | ||
| + | |||
| + | |||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | Die Zahl 4 wird bei 100 maligem Würfeln 26 Mal gewürfelt. Die relative Häufigkeit beträgt '''<math>\frac{26}{100}</math>'''. In Prozent sind das '''26'''% | + | Die Zahl 4 wird bei 100-maligem Würfeln 26 Mal gewürfelt. Die relative Häufigkeit beträgt '''<math>\frac{26}{100}</math>'''. In Prozent sind das '''26'''% |
<br /> | <br /> | ||
| − | Die relative Häufigkeit der Zahl 3 beträgt bei 50 maligem Würfeln <math>\frac{1}{10}</math>. Die 3 wurde also '''5''' | + | Die relative Häufigkeit der Zahl 3 beträgt bei 50-maligem Würfeln <math>\frac{1}{10}</math>. Die 3 wurde also '''5''' Mal gewürfelt. |
<br /> | <br /> | ||
| − | Die Zahl 8 wird bei 25 maligem würfeln 5 Mal gewürfelt. Ihre | + | Eine Münze wird 5 Mal geworfen. 3 Mal landet sie auf der Kopfseite, 2 Mal auf der Zahlseite. Die relative Häufigkeit, dass die Münze auf der Zahlseite landet beträgt '''40'''%. |
| + | <br /> | ||
| + | Die Zahl 8 wird bei 25-maligem würfeln 5 Mal gewürfelt. Ihre relative Häufigkeit beträgt '''20'''% oder '''<math>\frac{10}{50}</math>'''. | ||
<br /> | <br /> | ||
Es wurde 50 Mal gewürfelt.Die absolute Häufigkeit der Zahl 6 beträgt '''24'''% also <math>\frac{12}{50}</math>. | Es wurde 50 Mal gewürfelt.Die absolute Häufigkeit der Zahl 6 beträgt '''24'''% also <math>\frac{12}{50}</math>. | ||
| + | <br /> | ||
| + | Aus einer Urne mit blauen, gelben und roten Kugeln werden 20 Kugeln blind herausgenommen. 7 davon sind blau. Die relative Häufigkeit eine blauen Kugel zu ziehen liegt also bei '''35'''%. | ||
| + | <br /> | ||
| + | Eine Münze wird 8 Mal geworfen. 3 Mal landet sie auf der Kopfseite, 5 Mal auf der Zahlseite. Die relative Häufigkeit, dass die Münze auf der Zahlseite landet beträgt '''62,5'''%. | ||
| + | <br /> | ||
| + | |||
| + | |||
</div> | </div> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ||
| + | <iframe src="https://learningapps.org/watch?app=1871453" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | <br /> | ||
| + | <br /> | ||
Aktuelle Version vom 10. Januar 2020, 11:55 Uhr
Zufallsexperimente
Definition:
Wenn der Ausgang eines Experiments nicht vorhergesagt werden kann, aber alle möglichen Ergebnisse bekannt sind, nennt man es ein Zufallsexperiment.
Beispiel:
Fast jeder wird im Alltag regelmäßig Ausführer eines Zufallsexperiments. Ein gutes Beispiel sieht man beim Spielen von "Mensch ärger dich nicht". Wenn ein Spieler an der Reihe ist, würfelt er, um mit seiner Figur vorrücken zu können. Dieses Würfeln ist ein Zufallsexperiment. Wie wir in der Definition gelernt haben, ist ein Merkmal von Zufallsexperimenten die Unbekanntheit der Ergebnisse. Dies trifft auch beim Würfeln zu, da der Spieler nicht wissen kann, welche Zahl er würfeln wird. Obwohl das Würfelergebnis noch unbekannt ist, besteht das zweite Merkmal eines Zufallsexperiments darin, dass alle möglichen Ergebnisse bekannt sind. So auch beim Würfeln: Da die Spieler wissen, dass ein Würfel 6 Seiten hat, wissen sie auch, dass die Ergebnisse 1,2,3,4,5 oder 6 möglich sind. Welches Ergebnis genau eintritt ist allerdings unbekannt.
Teste, ob du Zufallsexperimente erkennen kannst:
Auswerten von Zufallsexperimenten
Zum Auswerten von Zufallsexperimenten betrachtet man die absolute und relative Häufigkeit.
Die absolute Häufigkeit gibt an, wie oft ein bestimmtes Ergebnis bei mehrmaliger Wiederholung eines Zufallsexperiments eintritt.
Die relative Häufigkeit gibt an, wie groß der Anteil der absoluten Häufigkeit/ des Ergebnisses an der Gesamtanzahl der Durchführung des Zufallsexperiments ist.
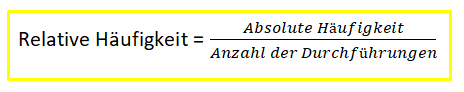
Beispiel:
Es wurde insgesamt 100 Mal gewürfelt.
100 = Anzahl der Durchführungen
| Augenzahl
|
|
|
|
|
|
|
| gewürfelte Anzahl ≙ absolute Häufigkeit
|
|
|
|
|
|
|
| Anteil der gewürfelten Anzahl an Zahl der Durchführungen ≙ relative Häufigkeit
|
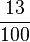 =13% |
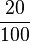 =20% |
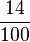 =14% |
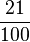 =21% |
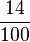 =14% |
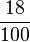 =18% |
Nett to know/Gut zu wissen: Empirisches Gesetz der großen Zahlen:
Nach einer großen Anzahl von Durchführungen eines Zufallsexperiments stabilisiert sich die relative Häufigkeit auf einen bestimmten Wert. Die relative Häufigkeit verändert sich also bei weiteren Durchführungen kaum.
Hier kannst du das Auswerten von Zufallsexperimenten üben:
| zum Vergleichen von Dezimalbrüchen | Zum nächsten Thema: Addition und Subtraktion gleichnamiger Brüche |
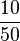
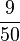
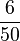
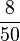
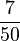
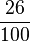 . In Prozent sind das 26%
. In Prozent sind das 26%
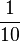 . Die 3 wurde also 5 Mal gewürfelt.
. Die 3 wurde also 5 Mal gewürfelt.
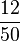 .
.

