Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Strecken und Spiegeln von Funktionsgraphen: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
{| | {| | ||
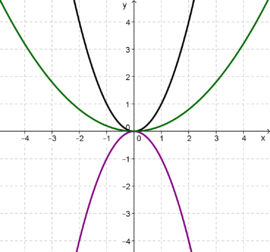
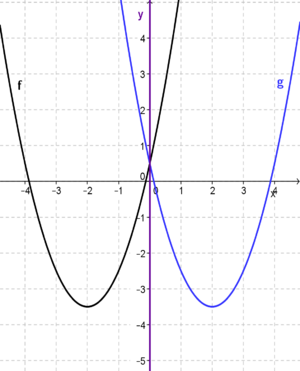
| − | | valign="top"|Auch das Strecken und Spiegeln von Parabeln ist bereits Thema der 9. Klasse. | + | | valign="top"|Auch das '''Strecken und Spiegeln von Parabeln''' ist bereits Thema der 9. Klasse. |
Du hast gelernt, dass die '''<span style="color: #008B00 ">Größe </span>'''des '''<span style="color: #FF7F00 ">Leitkoeffizienten</span>''', also des Koeffizienten <br /> | Du hast gelernt, dass die '''<span style="color: #008B00 ">Größe </span>'''des '''<span style="color: #FF7F00 ">Leitkoeffizienten</span>''', also des Koeffizienten <br /> | ||
'''<span style="color: #FF7F00 ">a</span>''' vor x² im Funktionsterm <br /> | '''<span style="color: #FF7F00 ">a</span>''' vor x² im Funktionsterm <br /> | ||
| Zeile 13: | Zeile 13: | ||
<br /> | <br /> | ||
Das '''<span style="color: #9A32CD">Vorzeichen</span>''' des Leitkoeffizienten ist entscheidend, ob die Parabel nach oben oder '''<span style="color: #9A32CD ">nach unten</span>''' geöffnet wird.<br /> | Das '''<span style="color: #9A32CD">Vorzeichen</span>''' des Leitkoeffizienten ist entscheidend, ob die Parabel nach oben oder '''<span style="color: #9A32CD ">nach unten</span>''' geöffnet wird.<br /> | ||
| − | Die Umkehrung des Vorzeichens des Leitkoeffizienten entspricht also einer Spiegelung an der x- Achse. | + | Die Umkehrung des Vorzeichens des Leitkoeffizienten entspricht also einer Spiegelung des jeweiligen Graphen an der x- Achse. |
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | Um dieses Wissen noch einmal zu wiederholen, folge diesem [http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Strecken_und_Spiegeln_von_Funktionsgraphen/ | + | Um dieses Wissen noch einmal zu wiederholen, folge diesem [http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Strecken_und_Spiegeln_von_Funktionsgraphen/Wiederholung:_Strecken_und_Spiegeln_von_Parabeln Link]. |
|width="1%"| | |width="1%"| | ||
| − | | [[Datei:Strecken und Spiegeln von Parabeln.png|270px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Strecken_und_Spiegeln_von_Funktionsgraphen/ | + | | [[Datei:Strecken und Spiegeln von Parabeln.png|270px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Strecken_und_Spiegeln_von_Funktionsgraphen/Wiederholung:_Strecken_und_Spiegeln_von_Parabeln]] |
|} | |} | ||
| Zeile 35: | Zeile 35: | ||
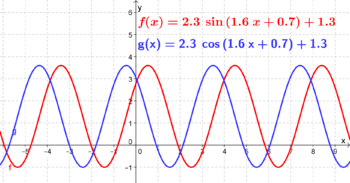
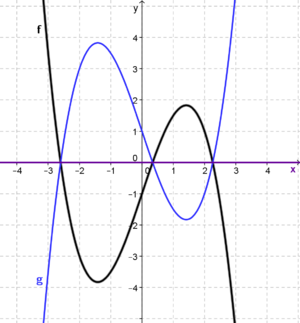
| valign="top"|In der 10. Klasse hast du dich bereits mit '''trigonometrischen Funktionen''', wie der '''<span style="color: red">Sinus-</span> '''und''' <span style="color: blue">Cosinusfunktion</span>''' beschäftigt.<br /> | | valign="top"|In der 10. Klasse hast du dich bereits mit '''trigonometrischen Funktionen''', wie der '''<span style="color: red">Sinus-</span> '''und''' <span style="color: blue">Cosinusfunktion</span>''' beschäftigt.<br /> | ||
<br /> | <br /> | ||
| − | Dabei hast du | + | Dabei hast du gelernt, dass Parameter im Funktionsterm Auswirkungen auf Lage und Aussehen des Graphen der Funktion haben.<br /> |
<br /> | <br /> | ||
| − | Dieses Wissen kannst du [http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Strecken_und_Spiegeln_von_Funktionsgraphen/ | + | Dieses Wissen kannst du [http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Strecken_und_Spiegeln_von_Funktionsgraphen/Wiederholung:_Trigonometrische_Funktionen hier] noch einmal auffrischen. |
|width="1%"| | |width="1%"| | ||
| − | | valign="top"|[[Datei:A sin(bx - c) + d.png|350px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Strecken_und_Spiegeln_von_Funktionsgraphen/ | + | | valign="top"|[[Datei:A sin(bx - c) + d.png|350px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Strecken_und_Spiegeln_von_Funktionsgraphen/Wiederholung:_Trigonometrische_Funktionen]] |
|} | |} | ||
| Zeile 78: | Zeile 78: | ||
|Link zurück=[[Manipulationen an Funktionen|Zurück zur Übersicht]] | |Link zurück=[[Manipulationen an Funktionen|Zurück zur Übersicht]] | ||
|Link vor=[[Manipulationen an Funktionen/Strecken und Spiegeln von Funktionsgraphen/Streckung in y- Richtung|Los geht´s mit der Streckung in y- Richtung]] | |Link vor=[[Manipulationen an Funktionen/Strecken und Spiegeln von Funktionsgraphen/Streckung in y- Richtung|Los geht´s mit der Streckung in y- Richtung]] | ||
| − | |Text Copyright=Manipulationen an Funktionen | + | |Text Copyright=<colorize>Manipulationen an Funktionen</colorize> |
}} | }} | ||
|} | |} | ||
Aktuelle Version vom 15. August 2013, 15:39 Uhr
|
|
|
Im weiteren lernst du, wie eine Funktion über die entsprechenden Parameter gestreckt oder gespiegelt werden kann.
Manipulationen an Funktionen
|