Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Strecken und Spiegeln von Funktionsgraphen: Unterschied zwischen den Versionen
| Zeile 28: | Zeile 28: | ||
|width="3%"| | |width="3%"| | ||
|valign="top"| [[Manipulationen an Funktionen/Strecken und Spiegeln von Funktionsgraphen/Spiegelung an der x- Achse|<big><center>Spiegelung an der x- Achse</center>]] | |valign="top"| [[Manipulationen an Funktionen/Strecken und Spiegeln von Funktionsgraphen/Spiegelung an der x- Achse|<big><center>Spiegelung an der x- Achse</center>]] | ||
| − | + | [[Datei:Spiegelung an der x- Achse.png|200px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Strecken_und_Spiegeln_von_Funktionsgraphen/Spiegelung_an_der_x-_Achse]] | |
|width="3%"| | |width="3%"| | ||
|valign="top"| [[Manipulationen an Funktionen/Strecken und Spiegeln von Funktionsgraphen/Spiegelung an der y- Achse|<big><center>Spiegelung an der y- Achse</center>]] | |valign="top"| [[Manipulationen an Funktionen/Strecken und Spiegeln von Funktionsgraphen/Spiegelung an der y- Achse|<big><center>Spiegelung an der y- Achse</center>]] | ||
Version vom 26. Mai 2013, 19:03 Uhr
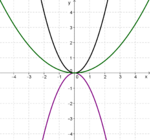
| Auch das Strecken und Spiegeln von Parabeln ist bereits Thema der 9. Klasse.
Du hast gelernt, dass der Leitkoeffizient, also der Koeffizient vor x², darauf Auswirkungen hat, wie weit oder eng die Parabel geöffnet ist. |
|
Im weiteren lernst du, wie eine Funktion über die entsprechenden Parameter gestreckt oder gespiegelt werden kann.
Fülle bei der Bearbeitung dieses Lernpfades das Arbeitsblatt aus, um alle wichtigen Informationen zu sammeln.
| |
|
|
|
| Zurück zur Übersicht | Los geht´s mit der Streckung in y- Richtung |
Manipulationen an Funktionen